详解

  • 小目标检测的一个常用思路是提升图片输入分辨率，来增强小目标的分辨率和生成高分辨率的特征图，但这会导致训练和验证极度费时。
  • 本文提出的PGAN方法对小目标生成高分辨率特征表示，使小目标的特征表示与大目标特征表示类似。
  • 生成器网络通过较前层提取细粒度特征将小目标分辨率较低的特征转换为分辨率较高的特征。
  • 判别器网络不仅用于生成小目标高分辨表示，同时证明带感知损失的生成高分辨率特征对检测准确率是有帮助的。
  • 生成器网络被训练欺骗辨别器通过产生最像大目标表征的小目标，同时提升检测准确率。
  • 辨别器被训练用于提升正确从实际大目标中分辨出生成的高分辨率表征，同时将定位准确率反馈给生成器。
  • 小目标检测典型应用领域：交通标志检测、行人检测

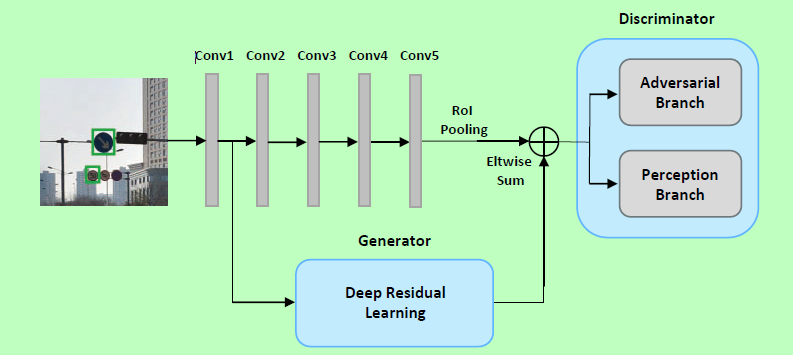
perception branch（感知分支）首先利用仅包含大目标的图片进行训练，然后利用仅包含小目标的图片进行训练，generator network 被训练用于对小目标生成高分辨率的类似大目标的表征。adversarial branch被训练用于区分生成的小目标高分辨率表征与实际大目标的原始表征。

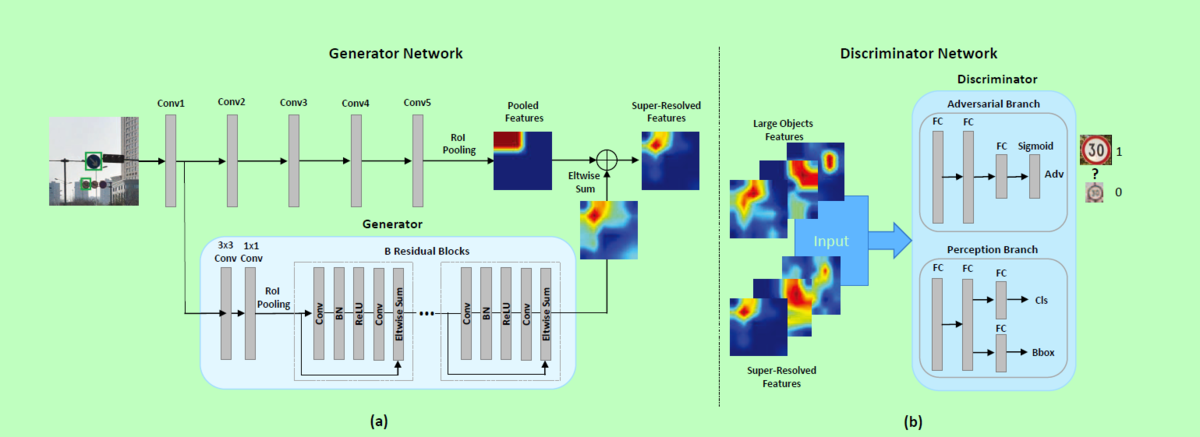
generator 从底层提取细粒度特征，放入深度残差网络，通过element-wise加和操作，将深度残差网络学习到的残差特征与conv5学习到的特征结合，得到高分辨率特征图；discriminator将大目标和小目标的高分辨特征作为输入，adversarial分支用于判断输入相片属于真的大目标的概率值，perception分支用于分类和边界框回归，验证从生成高分辨率特征获得的检测准确率提升。

损失函数

$F_{l}$和 $F_{s}$代表大目标和小目标特征，$G$和$D$代表生成器和判别器，$\Theta_{g}$和$\Theta_{a}$代表生成器和判别器的网络参数

  • 生成器
    $\Theta_{g}=\arg \min _{\Theta_{g}} L_{d i s}\left(G_{\Theta_{g}}\left(F_{s}\right)\right)$
    $L_{d i s}$是判别器网络产生的对抗性损失$L_{d i s_{-} a}$和感知损失$L_{d i s_ p}$的加权组合
    $L_{d i s}=w_{1} \times L_{d i s_{-} a}+w_{2} \times L_{d i s_{p}}$（作者设w1和w2为1）

    • 对抗性损失
      $L_{d i s_{-}a}=-\log D_{\Theta_{a}}\left(G_{\Theta_{g}}\left(F_{s}\right)\right)$（使$D_{\Theta_{a}}\left(G_{ \Theta_{g}}\left(F_{s}\right)\right)$尽可能大）

    • 感知损失

      $L_{d i s_{-p}}=L_{c l s}(p, g)+1[g \geq 1] L_{l o c}\left(r_{g}, r^{*}\right)$

      $L_{c l s}$和$L_{l o c}$是分类和边界框回归的损失

      感知分支输出K + 1个类别的类别级别置信度$p=\left(p_{0}, \dots, p_{k}\right)$，对于每个K对象类，边界框回归偏移$r_{k} = \left(r_{x}^{k}, r_{y}^{k}, r_{w}^{k}, r_{h}^{k}\right)$，真实类别为$g$，真实边界框回归目标$r^{*}$

  • 判别器网络的对抗分支：
    $\Theta_{a}=\arg \min _{\Theta_{a}} L_{a}\left(G_{\Theta_{g}}\left(F_{s}\right), F_{l}\right)$
    $L_{a}=-\log D_{\Theta_{a}}\left(F_{l}\right)-\log \left(1-D_{\Theta_{a}}\left(G_{\Theta_{g}}\left(F_{s}\right)\right)\right)$
    区分当前生成的小对象超分辨表示和原始对象与真实大对象之间的差异。 即使$D_{\Theta_{a}}$尽可能大，$D _{\Theta_{a}}\left(G _{Theta_{g}}\left(F_{s}\right)\right)$尽可能小。

联合对抗损失
$\begin{array}{rl}{\min _{G} \max _{D}} & {L(D, G) \triangleq \mathbb{E}_{F_{l} \sim p_{ \text {data(F }\left._{l}\right)}} \log D\left(F_{l}\right)} \\ {} & {+\mathbb{E}_{F_{s} \sim p_{F_{s}}}\left(F_{s} | f\right)[\log (1-D(\underbrace{F_{s}+G\left(F_{s} | f\right)}_{\text {residual learning }}))]}\end{array}$

即G的目标是使它最小，D的目标使它最大，由于$F_{s}$中包含的信息有限。因此，引入了一个新的条件生成器模型，该模型以额外的辅助信息为条件，即小对象$f$的低级特征，生成器从中通过残差学习在大对象和小对象表示之间生成残差表示。

个人理解：