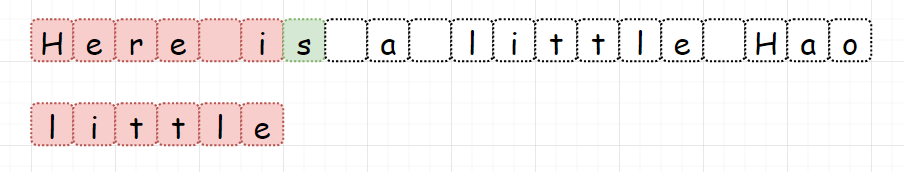本系列是本人在刷题过程中，参考《小浩算法》的题型分类所做。由于小浩在大多数题目并未使用统一的语言实现，这里本人给出了Python和Java的实现。目前Python实现已完成，Java实现仍在更新中。若有错误或者更好的解决方法，欢迎提出。

数组系列

1.交集

此题可以看成是一道传统的映射题（map映射），为什么可以这样看呢，因为我们需找出两个数组的交集元素，同时应与两个数组中出现的次数一致。这样就导致了我们需要知道每个值出现的次数，所以映射关系就成了<元素,出现次数>

[第349题] 给定两个数组，编写一个函数来计算它们的交集。

  • 示例 1：
    输入：nums1 = [1,2,2,1], nums2 = [2,2]
    输出：[2]

  • 示例 2：
    输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
    输出：[9,4]

说明： 输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序。

方法一：映射字典

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Python
class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        key = {}
        result=[]

        for v in nums1:
        	#遍历nums1，初始化字典key
            if v not in key:
                key[v] = 1


        for v in nums2:
            if v in key:
            	#如果元素相同，将其存入result中，并将出现次数减1
                if key[v] > 0:
                    key[v] -= 1
                    result.append(v)
        return result

执行耗时:60 ms,击败了74.80% 的Python3用户
内存消耗:13.4 MB,击败了70.92% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Map<Integer, Integer> map = new HashMap<>();
        int[] res = new int[nums2.length];
        int count = 0;
        //getOrDefault()，当Map集合中有这个key时，就使用这个key值，如果没有就使用默认值defaultValue
        for(int num: nums1) map.put(num, map.getOrDefault(num, 1));
        for(int num: nums2){
            if(map.getOrDefault(num, -1) > 0){
                map.put(num, map.get(num)-1);
                res[count++] = num;
            }
        }
        //返回指定长度的新数组对象
        return Arrays.copyOf(res, count);

    }
}

执行用时：3 ms, 在所有 Java 提交中击败了84.57% 的用户
内存消耗：38.9 MB, 在所有 Java 提交中击败了7.70% 的用户

方法二：set函数

1
2
3
4
5
6
#Python
class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
    	#set转化成无重复元素的集合取交集
        result = set(nums1).intersection(set(nums2))
        return list(result)

执行耗时:64 ms,击败了57.06% 的Python3用户
内存消耗:13.3 MB,击败了88.25% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//Java
class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> map = new HashSet<>();
        int[] res = new int[nums2.length];
        int count = 0;
        for(int num: nums1) map.add(num);
        for(int num: nums2){
            if(map.contains(num)){
                res[count++] = num;
                map.remove(num);
            }
        }
        //返回指定长度的新数组对象
        return Arrays.copyOf(res, count);

    }
}

执行用时：2 ms, 在所有 Java 提交中击败了94.86% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了58.09% 的用户

[第350题] 给定两个数组，编写一个函数来计算它们的交集。

  • 示例 1：
    输入：nums1 = [1,2,2,1], nums2 = [2,2]
    输出：[2]

  • 示例 2：
    输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
    输出：[9,4]

说明：输出结果中每个元素出现的次数，应与元素在两个数组中出现次数的最小值一致。我们可以不考虑输出结果的顺序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#Python
class Solution:
    def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
        key = {}
        result = []

        for v in nums1:
            #遍历nums1，初始化字典key
            if v not in key:
                key[v] = 1
            else:
                key[v] += 1

        for v in nums2:
            if v in key:
                #如果元素相同，将其存入result中，并将出现次数减1
                if key[v] > 0:
                    key[v] -= 1
                    result.append(v)

        return result

执行耗时:52 ms,击败了97.73% 的Python3用户
内存消耗:13.5 MB,击败了36.24% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//Java
class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        Map<Integer, Integer> map = new HashMap<>();
        int[] res = new int[nums2.length];
        int count = 0;
        for (int num : nums1) map.put(num,map.getOrDefault(num,0) + 1) ;
        for (int num : nums2){
            if(map.getOrDefault(num, -1) > 0){
                res[count++] = num ;
                map.put(num,map.get(num) -1) ;
            }
        }
        //返回指定长度的新数组对象
        return Arrays.copyOf(res, count);

    }
}

执行用时：3 ms, 在所有 Java 提交中击败了73.45% 的用户
内存消耗：38.8 MB, 在所有 Java 提交中击败了16.45% 的用户

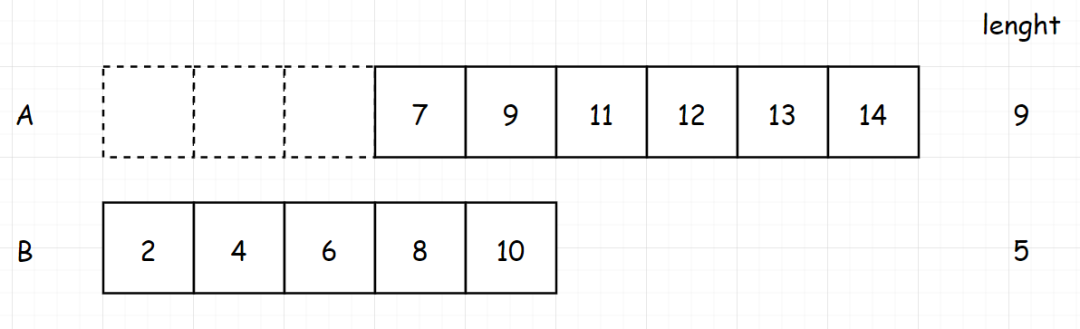
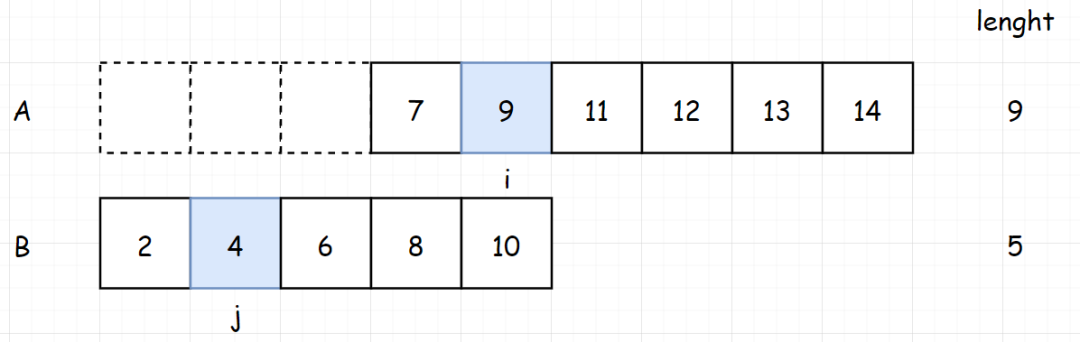
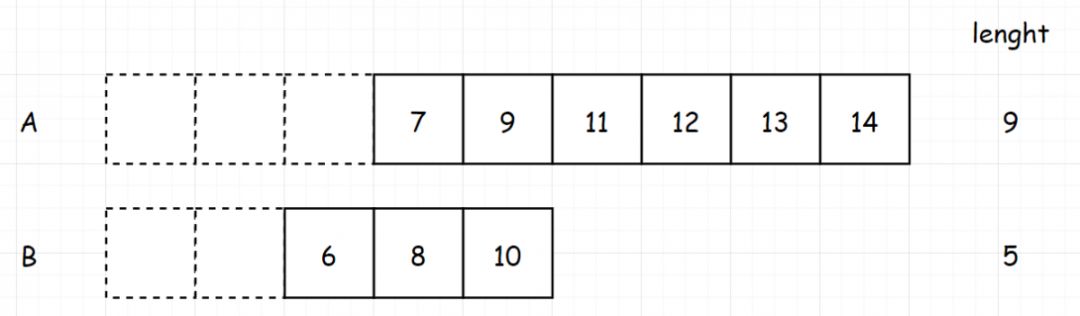
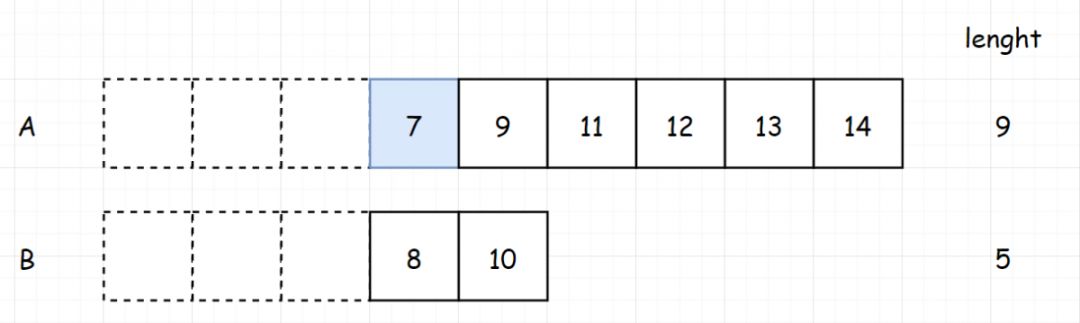
[题目进阶] 如果给定的数组已经排好序呢？你将如何优化你的算法？假如两个数组都是有序的，分别为：arr1 = [1,2,3,4,4,13]，arr2 = [1,2,3,9,10]

对于两个已经排序好数组的题，我们可以很容易想到使用双指针的解法

设定两个为0的指针，比较两个指针的元素是否相等。如果指针的元素相等，我们将两个指针一起
向后移动，并且将相等的元素放入空白数组。

如果两个指针的元素不相等，我们将小的元素的指针后移。继续进行判断。

反复以上步骤，直到任意一个数组终止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Python
class Solution:
    def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
        nums1.sort()
        nums2.sort()
        result = []
        i = 0
        j = 0
        while i < len(nums1) and j < len(nums2):
            if nums1[i] == nums2[j]:
                result.append(nums1[i])
                i += 1
                j += 1
            elif nums1[i] < nums2[j]:
                i += 1
            else:
                j += 1

        return result

执行耗时:68 ms,击败了46.68% 的Python3用户
内存消耗:13.4 MB,击败了44.53% 的Python3用户

2.最长公共前缀

我们要想寻找最长公共前缀，那么首先这个前缀是公共的，我们可以从任意一个元素中找到它。
假定我们现在就从一个数组中寻找最长公共前缀，那么首先，我们可以将第一个元素设置为基准
元素x0。假如数组为[“flow”,”flower”,”flight”]，flow就是我们的基准元素x0。

然后我们只需要依次将基准元素和后面的元素进行比较（假定后面的元素依次为x1,x2,x3….），不断更
新基准元素，直到基准元素和所有元素都满足最长公共前缀的条件，就可以得到最长公共前缀。

具体比对过程如下：

如果strings.Index(x1,x) == 0，则直接跳过（因为此时x就是x1的最长公共前缀），对比下一个元
素。（如flower和flow进行比较）

如果strings.Index(x1,x) != 0, 则截取掉基准元素x的最后一个元素，再次和x1进行比较，直至满足
string.Index(x1,x) == 0，此时截取后的x为x和x1的最长公共前缀。（如flight和flow进行比较，依
次截取出flow-flo-fl，直到fl被截取出，此时fl为flight和flow的最长公共前缀）

[第14题] 编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀，返回空字符串 “”。

  • 示例 1:
    输入: [“flower”,”flow”,”flight”]
    输出: “fl”

  • 示例 2:
    输入: [“dog”,”racecar”,”car”]
    输出: “”
    解释: 输入不存在公共前缀。

说明: 所有输入只包含小写字母 a-z 。

方法一：比对基准元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Python
class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        if len(strs) < 1:
            return ""
        else:
            #基准元素
            result = strs[0]
        #基准元素和后面的元素进行比较
        for k in strs[1:]:
            # find:在[beg, end]范围内查找substring，找到返回substr的起始下标，否则返回-1。
            # 前缀起始坐标必须为0开始，中间不算
            while k.find(result) != 0:
                if len(result) == 0:
                    return ''
                else:
                    #调整基准元素
                    result = result[:-1]
        return result

执行耗时:32 ms,击败了98.27% 的Python3用户
内存消耗:13.4 MB,击败了56.76% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//Java
class Solution {
    public String longestCommonPrefix(String[] strs) {
        //设置基准元素
        if(strs.length < 1) return "";
        String res = strs[0];
        //与后续字符串比较
        for(int i=1; i<strs.length; i++){
            //若不包含，则缩小范围
             while(!strs[i].startsWith(res)){
                if(res.length() == 0) return "";
                res = res.substring(0, res.length()-1);
            }
        }
        return res;

    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.7 MB, 在所有 Java 提交中击败了30.89% 的用户

方法二：利用ASCII码

利用python的max()和min()，在Python里字符串是可以比较的，按照ascII值排，举例abb， aba，abac，最大为abb，最小为aba。所以只需要比较最大最小的公共前缀就是整个数组的公共前缀

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        if not strs:
            return ""
        s1 = min(strs)
        s2 = max(strs)
        for i, x in enumerate(s1):
            if x != s2[i]:
                return s2[:i]
        return s1

执行耗时:44 ms,击败了61.62% 的Python3用户
内存消耗:13.3 MB,击败了85.07% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Java
class Solution {
    public String longestCommonPrefix(String[] strs) {
        if(strs.length < 1) return "";
        String min = strs[0];
        String max = strs[0];
        for(String s: strs){
            //若字符串等于参数字符串、则返回0，字符串小于参数字符串、则返回值小于0，字符串大于参数字符串、返回值大于0。
            if(s.compareTo(max) > 0) max = s;
            if(s.compareTo(min) < 0) min = s;
        }
        for(int i=0; i<min.length(); i++){
            if(min.charAt(i) != max.charAt(i)) return min.substring(0, i);
        }
        return min;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了85.32% 的用户
内存消耗：36.8 MB, 在所有 Java 提交中击败了20.75% 的用户

方法三：利用zip函数

利用python的zip函数，把str看成list然后把输入看成二维数组，左对齐纵向压缩，然后把每项利用集合去重，之后遍历list中找到元素长度大于1之前的就是公共前缀

比如strs=[“flow”,”flower”,”flight”]，则zip(*strs)将依次取出[‘f’,’f’,’f’]、[‘l’,’l’,’l’]、……、[‘’, ‘r’,’t’]，通过set去重，则[‘f’]、[‘l’]、……、[‘’, ‘r’,’t’]，长度大于1之前的就是公共前缀

1
2
3
4
5
6
7
8
9
10
11
12
13
#Python
class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        if not strs:
            return ""
        ss = list(map(set, zip(*strs)))
        res = ""
        for i, x in enumerate(ss):
            x = list(x)
            if len(x) > 1:
                break
            res = res + x[0]
        return res

执行耗时:40 ms,击败了81.85% 的Python3用户
内存消耗:13.4 MB,击败了50.03% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//Java
class Solution {
    public String longestCommonPrefix(String[] strs) {
        String res = "";
        List<Set<Character>> ss = new ArrayList<>();
        int maxLength = 0;
        for(String s: strs){
            if(s.length() > maxLength) maxLength = s.length();
        }
        for(int i=0; i<maxLength; i++){
            Set<Character> set = new HashSet<>();
            for(String s: strs){
                if(i < s.length()) set.add(s.charAt(i));
                else set.add(' ');
            }
            ss.add(set);
        }
        for(Set<Character> set: ss){
            if(set.size() > 1) break;
            for(char s: set) res += s;
        }
        return res;
    }
}

执行用时：16 ms, 在所有 Java 提交中击败了5.83% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了5.05% 的用户

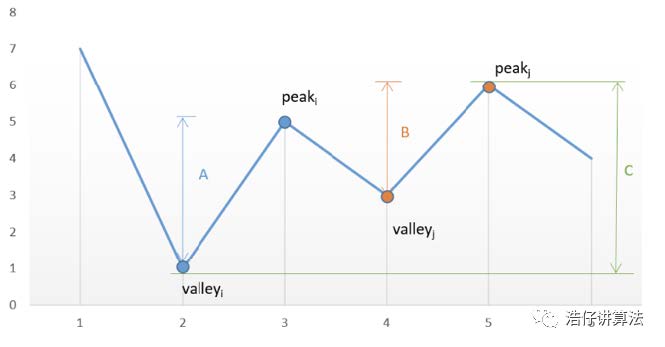
3.买卖股票的最佳时机

[第122题] 给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

  • 示例 1: 输入: [7,1,5,3,6,4]
    输出: 7
    解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

  • 示例 2:
    输入: [1,2,3,4,5]
    输出: 4
    解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

  • 示例 3:
    输入: [7,6,4,3,1]
    输出: 0
    解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

1、不能参与多笔交易。换句话讲，我们只能在手上没有股票的时候买入，也就是必须在再次购买前出
售掉之前的股票。像我们平时买股票时的追涨杀跌是不可以的。

2、尽可能地多进行交易。这个非常好理解。像是黄金，一年基本上都有2-3次涨跌。我们只要把握住机
会，在每一次涨跌的时候，低价卖入高价卖出，就可以使利益达到最大化。这个条件也是相当重要的，
如果我们把这里变成，最多完成两笔交易，就变成另一道题。

假设给定的数组为：[7, 1, 5, 3, 6, 4] 我们将其绘制成折线图，，我们要在满足1和2的条件下获取最大利益，其实就是尽可能多的低价买入高价卖出。而每一次上升波段，其实就是一次低价买入高价卖出。而我们没有限制交易次数，也就是我们需要求出所有的上升波段的和。如图里就是A+B，也就是（5-1）+（6-3） = 7，就是我们能获取到的最大利益。

方法一：贪心算法

只要今天价格小于明天价格就在今天买入然后明天卖出

1
2
3
4
5
6
7
8
#Python
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        profit = 0
        for i in range(len(prices)-1):
            if prices[i] < prices[i+1]:
                profit += (prices[i+1] - prices[i])
        return  profit

执行耗时:84 ms,击败了53.70% 的Python3用户
内存消耗:14.7 MB,击败了38.34% 的Python3用户

1
2
3
4
5
6
7
8
9
10
//Java
class Solution {
    public int maxProfit(int[] prices) {
        int profit=0;
        for(int i=0; i<prices.length-1; i++){
            if(prices[i]<prices[i+1]) profit+=(prices[i+1]-prices[i]);
        }
        return profit;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了99.57% 的用户
内存消耗：38.1 MB, 在所有 Java 提交中击败了79.49% 的用户

方法二：DP动态规划

第i天只有两种状态，不持有或持有股票，当天不持有股票的状态可能来自昨天卖出或者昨天也不持有，同理，当天持有股票的状态可能来自昨天买入或者昨天也持有中，取最后一天的不持有股票状态就是问题的解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Python
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        if len(prices) < 2:
            return 0
        dp = [[0]*2 for _ in range(len(prices))]
        # dp[i][0]表示第i天不持有股票, dp[i][1]表示第i天持有股票
        dp[0][0] = 0
        dp[0][1] = -prices[0]
        for i in range(1, len(prices)):
            #不持有股票分为：1.1一直都不买入仍是昨天的未持有 2.今天卖出，即昨天加今天卖出的钱
            dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
            #持有股票分为：1.昨天没有持有，今天买入 2.昨天已买入一直持有着
            dp[i][1] = max(dp[i-1][0]-prices[i], dp[i-1][1])
        return  dp[-1][0]

执行耗时:136 ms,击败了5.26% 的Python3用户
内存消耗:16.4 MB,击败了5.02% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i = 1; i< prices.length; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+prices[i]); 
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-prices[i]);
        }
        return dp[prices.length-1][0];
    }
}

执行用时：4 ms, 在所有 Java 提交中击败了19.71% 的用户
内存消耗：38 MB, 在所有 Java 提交中击败了91.41% 的用户

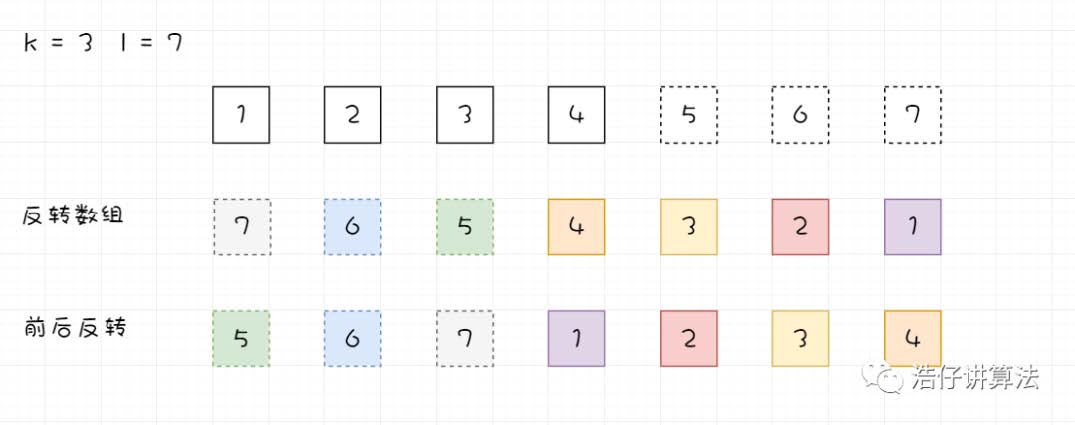
4.旋转数组

[第189题] 给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

  • 示例 1:
    输入: [1,2,3,4,5,6,7] 和 k = 3
    输出: [5,6,7,1,2,3,4]
    解释:向右旋转 1 步: [7,1,2,3,4,5,6]，向右旋转 2 步: [6,7,1,2,3,4,5]，向右旋转 3 步: [5,6,7,1,2,3,4]
  • 示例 2:
    输入: [-1,-100,3,99] 和 k = 2
    输出: [3,99,-1,-100]
    解释: 向右旋转 1 步: [99,-1,-100,3]，向右旋转 2 步: [3,99,-1,-100]

说明: 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。 要求使用空间复杂度为 O(1) 的原地算法。

这个方法基于这个事实：若我们需要将数组中的元素向右移动 k 个位置， 那么 k%l (l为数组长
度) 的尾部元素会被移动到头部，剩下的元素会被向后移动。

通过观察我们可以得到，我们只需要将所有元素反转，然后反转前 k 个元素，再反转后面l-k个元素，就能得到想要的结果。

方法一：翻转三次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Python
class Solution:
    def rotate(self, nums: List[int], k: int) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        n = len(nums)
        k %= n
        # 定义反转函数
        def switch(a, b):
            while (a<b):    # 从两头往中间交换
                nums[a], nums[b] = nums[b], nums[a]
                a += 1
                b -= 1
        # 三次反转
        switch(0, n-1)  # 反转整体
        switch(0, k-1)    # 反转前k个元素
        switch(k, n-1)    # 反转后面元素
        return nums

执行耗时:36 ms,击败了94.96% 的Python3用户
内存消耗:13.5 MB,击败了76.57% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
    public void rotate(int[] nums, int k) {
        k = k % nums.length;
        reverse(nums, 0, nums.length-1);
        reverse(nums, 0, k-1);
        reverse(nums, k, nums.length-1);
    }

    public void reverse(int[] nums, int start, int end) {
            while(start < end){
                int tmp = nums[start];
                nums[start] = nums[end];
                nums[end] = tmp;
                start++;
                end--;
            }
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：39 MB, 在所有 Java 提交中击败了45.62% 的用户

方法二：利用切片翻转

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def rotate(self, nums: List[int], k: int) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        k = k % len(nums)
        nums.reverse()
        nums[:k] = reversed(nums[:k])
        nums[k:] = reversed(nums[k:])
        return nums

执行耗时:40 ms,击败了85.56% 的Python3用户
内存消耗:13.6 MB,击败了27.15% 的Python3用户

方法三：利用切片移位（不考虑原地算法）

1
2
3
4
5
6
7
8
9
#Python
class Solution:
    def rotate(self, nums: List[int], k: int) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        k = k % len(nums)
        nums[:] = nums[-k:] + nums[:-k]
        return nums

执行耗时:40 ms,击败了85.56% 的Python3用户
内存消耗:13.6 MB,击败了44.31% 的Python3用户

5.原地删除

[第27题] 给你一个数组nums和一个值val，你需要原地移除所有数值等于val的元素，并返回移除后数组的新长度。 不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

  • 示例 1:
    给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
    你不需要考虑数组中超出新长度后面的元素。
  • 示例 2:
    给定 nums = [0,1,2,2,3,0,4,2], val = 2,函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
    注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        # 应使用逆序
        # 如果是正序的话，删除一个索引所对应的值后
        # python会自动吧删除的位置补上来
        # 这样就会导致从删除位位置到最后一位的索引和原索引相差1个
        for i in range(len(nums)-1, -1, -1):
            if nums[i] == val:
                del nums[i]
        return len(nums)

执行耗时:40 ms,击败了72.46% 的Python3用户
内存消耗:13.4 MB,击败了33.88% 的Python3用户

因为题目说了不需要考虑数组中超出新长度后面的元素，所以不需要真的移除，只要将其值覆盖即可

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int removeElement(int[] nums, int val) {
        int count=0;
        for(int i=0;i<nums.length;i++){
            if(nums[i]!=val){
                nums[count]=nums[i];
                count++;
            }
        }
        return count;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：37.3 MB, 在所有 Java 提交中击败了8.49% 的用户

[第26题] 给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

  • 示例 1:
    给定数组 nums = [1,1,2], 函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。 你不需要考虑数组中超出新长度后面的元素。
  • 示例 2:
    给定 nums = [0,0,1,1,1,2,2,3,3,4],函数应该返回新的长度 5, 并且原数组nums的前五个元素被修改为 0, 1, 2, 3, 4。
    你不需要考虑数组中超出新长度后面的元素。

这道题的重点是原地两个字，也就是要求必须在 O(1) 的空间下完成。并且题中已经告知了数组为有序数组，这样重复的元素一定是连在一起的，我们只需要一个一个移除重复的元素即可

方法一：循环移除

1
2
3
4
5
6
7
#Python
class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        for i in range(len(nums)-1, 0, -1):
            if nums[i] == nums[i-1]:
                del nums[i]
        return len(nums)

执行耗时:44 ms,击败了88.67% 的Python3用户
内存消耗:14.2 MB,击败了96.20% 的Python3用户

与27题同理

1
2
3
4
5
6
7
8
9
10
11
//Java
class Solution {
    public int removeDuplicates(int[] nums) {
        int count = 0;
        for(int i=0; i < nums.length-1; i++){
            if(nums[i]!=nums[i+1]) nums[++count] = nums[i+1];

        }
        return ++count;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了80.44% 的用户
内存消耗：40.4 MB, 在所有 Java 提交中击败了19.16% 的用户

方法二：set函数（不考虑原地算法）

1
2
3
4
5
#Python
class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        nums[:] = sorted(list(set(nums)))
        return len(nums)

执行耗时:32 ms,击败了99.68% 的Python3用户
内存消耗:14.4 MB,击败了64.71% 的Python3用户

6.加一

[第66题] 给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。最高位数字存放在数组的首位，数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外，这个整数不会以零开头。

  • 示例 1:
    输入: [1,2,3]
    输出: [1,2,4]
    解释: 输入数组表示数字 123。

  • 示例 2:
    输入: [4,3,2,1]
    输出: [4,3,2,2]
    解释: 输入数组表示数字 4321。

根据题目，我们需要加一！没错，加一很重要。因为它只是加一，所以我们会考虑到两种情况：

普通情况，除9之外的数字加1。
特殊情况，9加1。（因为9加1需要进位）

所以我们只需要模拟这两种运算，就可以顺利进行求解！

方法一：模拟运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Python
class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        addon = 0
        for i in range(len(digits)-1, -1, -1):
            digits[i] += addon
            # 将进位归0
            addon = 0
            # 个位加1
            if i == len(digits) - 1:
                digits[i] += 1
            # 逢十进一
            if digits[i] == 10:
                addon = 1
                digits[i] = 0
        #类似99，或者999，我们需要进行扩充数组
        if addon == 1:
            digits.insert(0, 1)
        return digits

执行耗时:40 ms,击败了70.94% 的Python3用户
内存消耗:13.4 MB,击败了46.46% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//Java
class Solution {
    public int[] plusOne(int[] digits) {
        int[] res = new int[digits.length+1];
        int addon = 0;
        for(int i=digits.length-1; i>=0; i--){
            if(i==digits.length-1) digits[i]++;
            res[i+1] = digits[i] + addon;
            addon = 0;
            if(res[i+1]==10){
                addon = 1;
                res[i+1] = 0;
            }
        }
        if(addon==1) res[0] = 1;
        return addon==1?res: Arrays.copyOfRange(res, 1, res.length);
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：37 MB, 在所有 Java 提交中击败了29.28% 的用户

方法二：利用Python特性

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        # 整形转字符
        digits = [str(i) for i in digits]
        # 拼接字符转数字
        digits = int("".join(digits))
        # 加1
        digits += 1
        # 数字转列表
        return list(map(int, str(digits)))

执行耗时:48 ms,击败了18.72% 的Python3用户
内存消耗:13.4 MB,击败了33.38% 的Python3用户

7.两数之和

[第1题] 给定一个整数数组nums和一个目标值target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

  • 示例:
    给定 nums = [2, 7, 11, 15], target = 9
    因为 nums[0] + nums[1] = 2 + 7 = 9
    所以返回 [0, 1]

方法一：暴力解法

首先我们拿到题目一看，马上可以想到暴力题解。我们只需要 “遍历每个元素 x，并查找是否存在一个值与 target - x 相等的目标元素。”

1
2
3
4
5
6
7
#Python
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i in range(len(nums)):
            if target-nums[i] in nums[i+1:]:
                return i, nums[i+1:].index(target-nums[i])+i+1
        return []

执行耗时:964 ms,击败了38.87% 的Python3用户
内存消耗:14.1 MB,击败了85.75% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
//Java
class Solution {
    public int[] twoSum(int[] nums, int target) {
        for(int i=0; i < nums.length-1; i++){
            int tmp = target - nums[i];
            for(int j=i+1; j < nums.length; j++){
                if(nums[j]==tmp) return new int[]{i, j};
            }
        }
        return null;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了44.60% 的用户

可以看到该种解题方式的时间复杂度过高，达到了O(n²)。为了对运行时间复杂度进行优化，我们需要一种更有效的方法来检查数组中是否存在目标元素。我们可以想到用哈希表的方式，通过以空间换取时间的方式来进行。

方法二：哈希表

首先先遍历数组nums，i 为当前下标。将每一个遍历的值放入字典中作为key。

同时，对每个值都判断字典中是否存在target-nums[i]的key值。

1
2
3
4
5
6
7
8
9
10
#Python
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hashmap = {}
        for index, num in enumerate(nums):
            another_num = target - num
            if another_num in hashmap:
                return [hashmap[another_num], index]
            hashmap[num] = index
        return []

执行耗时:52 ms,击败了91.51% 的Python3用户
内存消耗:14.6 MB,击败了37.49% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
//Java
class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int i=0; i<nums.length; i++){
            if(map.containsKey(target-nums[i])) return new int[]{map.get(target-nums[i]), i};
            map.put(nums[i], i);
        }
        return null;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了34.68% 的用户

8.三数之和

[第15题] 给你一个包含n个整数的数组nums，判断nums中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。 注意：答案中不可以包含重复的三元组。

  • 示例：
    给定数组 nums = [-1, 0, 1, 2, -1, -4]，
    满足要求的三元组集合为：
    [
    [-1, 0, 1],
    [-1, -1, 2]
    ]

本题的暴力题解可以仿照二数之和，直接三层遍历，取和为0的三元组，并记录下来，最后再去重。但是作为一个有智慧的人，我们不能这么去做。

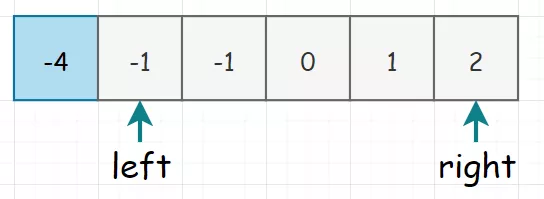
假若我们的数组为：[-1, 0, 1, 2, -1, -4]
首先我们先把数组排个序，因为我们要同时找三个数，所以采取固定一个数，同时用双指针来查找另外两个数的方式。所以初始化时，我们选择固定第一个元素（当然，这一轮走完了，这个蓝框框我们就要也往前移动），同时将下一个元素和末尾元素分别设上 left 和 right 指针。画出图来就是下面这个样子：

因为我们已经排好了序，如果固定下来的数（上面蓝色框框）本身就大于 0，那三数之和必然无法等于 0。
现在我们的排序就发挥出用处了，如果和大于0，那就说明 right 的值太大，需要左移。如果和小于0，那就说明 left 的值太小，需要右移。

其中：在第6行时，因为三数之和大于0，所以right进行了左移。最后一行，跳过了重复的-1。
除了固定下来的i值（蓝框框），left 和 right 当然也是需要处理重复的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#Python
class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        if len(nums) < 3:
            return []
        # 进行排序
        nums.sort()
        res = []
        for i in range(len(nums)):
            # 固定值大于0退出循环
            if nums[i] > 0:
                break
            # 过滤固定值重复
            if i > 0 and nums[i] == nums[i - 1]:
                continue
            # 左指针
            L = i + 1
            # 右指针
            R = len(nums) - 1
            while L < R:
                # 满足条件添加res
                if nums[i] + nums[L] + nums[R] == 0:
                    res.append([nums[i], nums[L], nums[R]])
                    #满足条件后，移动双指针，跳过重复的
                    while L < R and nums[L] == nums[L + 1]:
                        L = L + 1
                    while L < R and nums[R] == nums[R - 1]:
                        R = R - 1
                    L = L + 1
                    R = R - 1
                # 三数之和大于0,右指针左移
                elif nums[i] + nums[L] + nums[R] > 0:
                    R = R - 1
                # 三数之和小于0,左指针右移
                else:
                    L = L + 1
        return res

执行耗时:836 ms,击败了79.07% 的Python3用户
内存消耗:16 MB,击败了43.03% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//Java
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(nums);
        for(int i = 0; i<nums.length-2; i++){
            if(nums[i] > 0) break;
            if(i > 0 && nums[i] == nums[i-1]) continue;
            int l = i + 1;
            int r = nums.length - 1;
            while(l < r){
                if(nums[i] + nums[l] + nums[r] == 0){
                    res.add(new ArrayList<Integer>(Arrays.asList(nums[i], nums[l], nums[r])));
                    while(l < r && nums[l] == nums[l+1]) l++;
                    while(l < r && nums[r] == nums[r-1]) r--;
                    l++;
                    r--;
                }
                else if(nums[i] + nums[l] + nums[r] > 0) r--;
                else l++;
            }
        }
        return res;
    }
}

执行用时：29 ms, 在所有 Java 提交中击败了31.84% 的用户
内存消耗：42.5 MB, 在所有 Java 提交中击败了48.86% 的用户

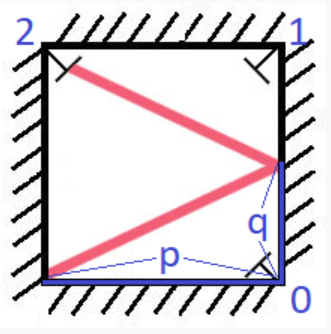
9.Z字形变换

[第6题] 将一个给定字符串根据给定的行数，以从上往下、从左到右进行 Z 字形排列。 比如输入字符串为 “LEETCODEISHIRING” 行数为 3 时，排列如下：
L C I R
E T O E S I I G
E D H N
之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如：”LCIRETOESIIGEDHN”。 请你实现这个将字符串进行指定行数变换的函数： string convert(string s, int numRows);

  • 示例 1:
    输入: s = “LEETCODEISHIRING”, numRows = 3
    输出: “LCIRETOESIIGEDHN”
  • 示例 2:
    输入: s = “LEETCODEISHIRING”, numRows = 4
    输出: “LDREOEIIECIHNTSG”
    解释:
    L D R
    E O E I I
    E C I H N
    T S G

根据 numRows 的大小来回进行放置即可（即从0到n-1，再从n-1到0）。具体的请看下图：


我们能看出来，每 2n-2 即为一个周期。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#Python
class Solution:
    def convert(self, s: str, numRows: int) -> str:
        if numRows == 1:
            return s
        temp = ['' for _ in range(numRows)]
        period = numRows * 2 - 2
        for index, value in enumerate(s):
            # 每2n-2为周期
            mod = index % period
            # 0到n-1
            if mod < numRows:
                temp[mod] += value
            # n-1到0
            else:
                temp[period - mod] += value
        return ''.join(temp)

执行耗时:56 ms,击败了95.52% 的Python3用户
内存消耗:13.6 MB,击败了16.18% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
    public String convert(String s, int numRows) {
        if(numRows < 2) return s;
        String[] tmp = new String[numRows];
        Arrays.fill(tmp, "");
        int period = numRows * 2 - 2;
        for(int i=0; i < s.length(); i++){
            int mod = i % period;
            if(mod < numRows) tmp[mod] += s.charAt(i);
            else tmp[period-mod] += s.charAt(i);
        }
        String res = "";
        for(String str: tmp){
            res += str;
        }
        return res;
    }
}

执行用时：18 ms, 在所有 Java 提交中击败了20.92% 的用户
内存消耗：39.5 MB, 在所有 Java 提交中击败了13.73% 的用户

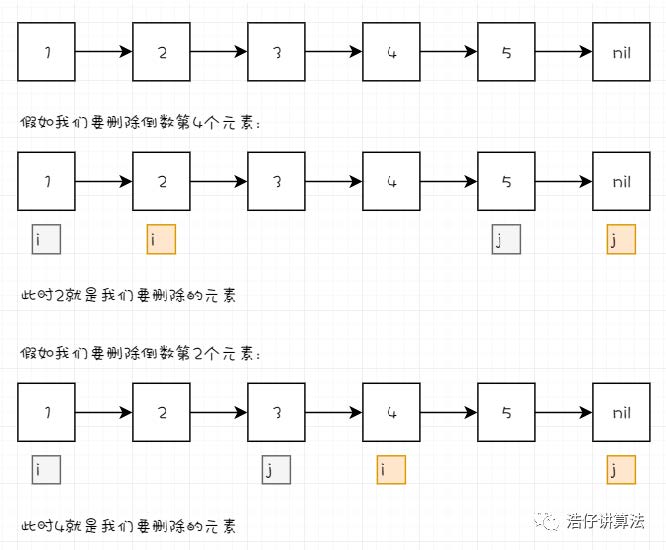
链表系列

1.删除链表倒数第N个节点

在链表的题目中，十道有九道会用到哨兵节点，所以我们先讲一下什么是哨兵节点。
哨兵节点，其实就是一个附加在原链表最前面用来简化边界条件的附加节点，它的值域不存储任何东
西，只是为了操作方便而引入。比如原链表为 a -> b -> c，则加了哨兵节点的链表即为 x -> a -> b > c。

那我们为什么需要引入哨兵节点呢?举个例子，比如我们要删除某链表的第一个元素，常见的删除链表
的操作是找到要删元素的前一个元素，假如我们记为pre。我们通过：

pre.Next = pre.Next.Next

来进行删除链表的操作。但是此时若是删除第一个元素的话，你就很难进行了，因为按道理来讲，此时
第一个元素的前一个元素就是nil（空的），如果使用pre就会报错。那如果此时你设置了哨兵节点的
话，此时的pre就是哨兵节点了。这样对于链表中的任何一个元素，你要删除都可以通过 pre.Next =
pre.Next.Next 的方式来进行，这就是哨兵节点的作用。

[第19题] 给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

  • 示例：
    给定一个链表: 1->2->3->4->5, 和 n = 2.
    当删除了倒数第二个节点后，链表变为 1->2->3->5.

说明： 给定的 n 保证是有效的。
进阶： 你能尝试使用一趟扫描实现吗？

首先我们思考，让我们删除倒数第N个元素，那我们只要找到倒数第N个元素就可以了，那怎么找
呢？我们只需要设置两个指针变量，中间间隔N-1元素。当后面的指针遍历完所有元素指向nil
时，前面的指针就指向了我们要删除的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Python
class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        # 思路：双指针法。
        slow = fast = head
        for i in range(n):  # 先让fast走n步
            fast = fast.next
        if fast == None:  # 若走了n步后为None，则表明删除的为head节点
            return head.next

        while fast.next != None:  # slow和fast同时往前走
            slow = slow.next  # 当fast走到头时，second即是要删除节点的前一个节点位置
            fast = fast.next
        slow.next = slow.next.next  # 删除该节点
        return head

执行耗时:40 ms,击败了82.68% 的Python3用户
内存消耗:13.4 MB,击败了31.27% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Java
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode res = new ListNode(0, head);
        ListNode fast = head;
        ListNode slow = res;
        int i = 0;
        while(fast.next!=null){
            fast=fast.next;
            i++;
            if(i >= n) slow = slow.next;   
        }
        slow.next = slow.next.next;
        return res.next;

    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.5 MB, 在所有 Java 提交中击败了33.64% 的用户

2.合并两个有序链表

[第21题] 将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

  • 示例：
    输入：1->2->4, 1->3->4
    输出：1->1->2->3->4->4

首先我们维护一个prehead的哨兵节点。我们其实只需要调整它的next指针。让它总是指向l1或者l2中较小的一个，直到l1或者l2任一指向null。这样到了最后，如果l1还是l2中任意一方还有余下元素没有用到，那余下的这些元素一定大于prehead已经合并完的链表（因为是有序链表）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#Python
class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        # 创建一个新链表
        cur = ListNode()
        # 设置哨兵节点
        result = cur
        # 指向两者中小的
        while l1 and l2:
            if l1.val < l2.val:
                cur.next = l1
                l1 = l1.next
            else:
                cur.next = l2
                l2 = l2.next
            cur = cur.next
        # 将其中一方剩余的添加进来
        if l1 is not None:
            cur.next = l1
        if l2 is not None:
            cur.next = l2
        return result.next

执行耗时:52 ms,击败了48.83% 的Python3用户
内存消耗:13.3 MB,击败了79.52% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//Java
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode res = new ListNode(0);
        ListNode p = res;
        while(l1!=null && l2!=null){
            if(l1.val<=l2.val){
                p.next = l1;
                l1 = l1.next;
            }else{
                p.next = l2;
                l2 = l2.next;
            }
            p = p.next;
        }
        if(l1!=null) p.next = l1;
        if(l2!=null) p.next = l2;
        return res.next;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.1 MB, 在所有 Java 提交中击败了10.58% 的用户

3.环形链表

[第141题] 给定一个链表，判断链表中是否有环。如果链表中有某个节点，可以通过连续跟踪next指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数pos来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果pos是 -1，则在该链表中没有环。注意：pos不作为参数进行传递，仅仅是为了标识链表的实际情况。 如果链表中存在环，则返回true 。 否则，返回false 。

  • 示例 1：输入：head = [3,2,0,-4], pos = 1
    输出：true
    解释：链表中有一个环，其尾部连接到第二个节点。
  • 示例 2：输入：head = [1,2], pos = 0
    输出：true
    解释：链表中有一个环，其尾部连接到第一个节点。
  • 示例 3：输入：head = [1], pos = -1
    输出：false
    解释：链表中没有环。

进阶：你能用O(1)（即，常量）内存解决此问题吗？

方法一：哈希表判定

思路：通过hash表来检测节点之前是否被访问过，来判断链表是否成环。

1
2
3
4
5
6
7
8
9
10
#Python
class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        hash = {}
        while head:
            if head in hash:
                return True
            hash[head] = 1
            head = head.next
        return False

执行耗时:64 ms,击败了58.42% 的Python3用户
内存消耗:16.4 MB,击败了32.63% 的Python3用户

方法二：双指针

本题标准解法！常识内容，必须掌握！

思路来源：先想象一下，两名运动员以不同速度在跑道上进行跑步会怎么样？相遇！好了，这道题你会
了。

解题方法：通过使用具有不同速度的快、慢两个指针遍历链表，空间复杂度可以被降低至 O(1)。慢指
针每次移动一步，而快指针每次移动两步。

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        slow, fast = head, head
        while fast and fast.next:
            # 慢指针，每次走一步; 快指针，每次走两步
            slow, fast = slow.next, fast.next.next
            # 快慢指针相遇，表示有环
            if fast is slow:
                return True
        return False

执行耗时:48 ms,击败了99.09% 的Python3用户
内存消耗:16.3 MB,击败了77.10% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
public class Solution {
    public boolean hasCycle(ListNode head) {
       ListNode fast = head;
       ListNode slow = head;
       while(fast!=null && fast.next!=null){
           slow = slow.next;
           fast = fast.next.next;
           if(fast==slow) return true;
       }
       return false;  
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：39.7 MB, 在所有 Java 提交中击败了13.26% 的用户

4.两数相加

[第2题] 给出两个非空的链表用来表示两个非负的整数。其中，它们各自的位数是按照逆序的方式存储的，并且它们的每个节点只能存储一位数字。如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。您可以假设除了数字 0 之外，这两个数都不会以 0 开头。

  • 示例：
    输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
    输出：7 -> 0 -> 8
    原因：342 + 465 = 807

加法肯定是从最低位到最高位进行相加，也就是这里的链表头到链表尾进行相加，所以需要遍历链表。

令 l1 和 l2 指向两个链表的头，用一个tmp值来存储同一位相加的结果，以及一个新的链表来存储tmp的值。

所有模拟运算的题目，都需要考虑进位。我们使用tmp携带进位的值到下一位的运算。自然，这里的链表也不能直接存储tmp的值了，而是要存储tmp%10的值。重复这个步骤，直到两个链表都遍历完成，并且 tmp 没有进位值。

因为我们没有构造哨兵节点，所以此时不太容易直接返回新链表。所以在整个流程的第一步，我们还需要用一个哨兵节点指向我们的新链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#Python
class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        list = ListNode()
        result = list
        tmp = 0
        while l1 or l2 or tmp != 0:
            if l1:
                tmp += l1.val
                l1 = l1.next
            if l2:
                tmp += l2.val
                l2 = l2.next
            list.next = ListNode(tmp % 10)
            tmp //= 10
            list = list.next
        return result.next

执行耗时:72 ms,击败了84.37% 的Python3用户
内存消耗:13.6 MB,击败了6.12% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//Java
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode res = new ListNode();
        ListNode p = res;
        int tmp = 0;
        while(l1!=null || l2!=null || tmp != 0){
            if(l1!=null){
                tmp += l1.val;
                l1 = l1.next;
            }
            if(l2!=null){
                tmp += l2.val;
                l2 = l2.next;
            }
            p.next = new ListNode(tmp % 10);
            tmp /= 10;
            p = p.next;
        }
        return res.next;
    }
}

执行用时：2 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.9 MB, 在所有 Java 提交中击败了49.86% 的用户

动态规划系列

关于动态规划的资料很多，官方的定义是指把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解。概念中的各阶段之间的关系，其实指的就是状态转移方程。很多人觉得DP难（下文统称动态规划为DP），根本原因是因为DP跟一些固定形式的算法不同（比如DFS、二分法、KMP），它没有实际的步骤规定第一步、第二步来做什么，所以准确来说，DP其实是一种解决问题的思想。

这种思想的本质是：一个规模比较大的问题（可以用两三个参数表示的问题），可以通过若干规模较小的问题的结果来得到的（通常会寻求到一些特殊的计算逻辑，如求最值等）。

那么我们应该如何通过子问题去得到大规模问题呢？这就用到了状态转移方程，我们一般看到的状态转移方程，基本都是这样：

1
2
3
4
5
>opt ：指代特殊的计算逻辑，通常为 max or min。
>i,j,k 都是在定义DP方程中用到的参数。
>dp[i] = opt(dp[i-1])+1
>dp[i][j] = w(i,j,k) + opt(dp[i-1][k])
>dp[i][j] = opt(dp[i-1][j] + xi, dp[i][j-1] + yj, ...)

每一个状态转移方程，多少都有一些细微的差别。这个其实很容易理解，世间的关系多了去了，不可能抽象出完全可以套用的公式。所以我个人其实不建议去死记硬背各种类型的状态转移方程。

1.爬楼梯

[第70题] 假设你正在爬楼梯。需要n阶你才能到达楼顶。每次你可以爬1或2个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定n是一个正整数。

  • 示例 1：
    输入： 2
    输出： 2
    解释： 有两种方法可以爬到楼顶。
  1. 1 阶 + 1 阶
  2. 2 阶
  • 示例 2：
    输入： 3
    输出： 3
    解释： 有三种方法可以爬到楼顶。
  1. 1 阶 + 1 阶 + 1 阶
  2. 1 阶 + 2 阶
  3. 2 阶 + 1 阶

通过分析我们可以明确，该题可以被分解为一些包含最优子结构的子问题，即它的最优解可以从其子问题的最优解来有效地构建。满足“将大问题分解为若干个规模较小的问题”的条件。所我们令dp[n]表示能到达第n阶的方法总数，可以得到如下状态转移方程：

dp[n]=dp[n-1]+dp[n-2]

上 1 阶台阶：有1种方式。
上 2 阶台阶：有1+1和2两种方式。
上 3 阶台阶：到达第3阶的方法总数就是到第1阶和第2阶的方法数之和。
上 n 阶台阶，到达第n阶的方法总数就是到第 (n-1) 阶和第 (n-2) 阶的方法数之和。

1
2
3
4
5
6
7
8
#Python
class Solution:
    def climbStairs(self, n: int) -> int:
        dp = [0, 1, 2]
        if n >= 3:
            for i in range(3, n+1):
                dp.append(dp[i-1] + dp[i-2])
        return dp[n]

执行耗时:36 ms,击败了87.16% 的Python3用户
内存消耗:13.4 MB,击败了50.33% 的Python3用户

1
2
3
4
5
6
7
8
9
10
//Java
class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i=2; i<=n; i++) dp[i] = dp[i-1] + dp[i-2];
        return dp[n]; 
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.3 MB, 在所有 Java 提交中击败了38.13% 的用户

2.最大子序和

[第53题] 给定一个整数数组nums，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

  • 示例:
    输入: [-2,1,-3,4,-1,2,1,-5,4]
    输出: 6
    解释: 连续子数组 [4,-1,2,1] 的和最大，为6。

首先我们分析题目，一个连续子数组一定要以一个数作为结尾，那么我们可以将状态定义成如下：

dp[i]：表示以nums[i]结尾的连续子数组的最大和。

根据状态的定义，我们继续进行分析：如果要得到dp[i]，那么nums[i]一定会被选取。并且dp[i]所表示的连续子序列与dp[i-1]所表示的连续子序列很可能就差一个nums[i] 。即：

dp[i] = dp[i-1]+nums[i] , if (dp[i-1] >= 0)

但是这里我们遇到一个问题，很有可能dp[i-1]本身是一个负数。那这种情况的话，如果dp[i]通过dp[i-1]+nums[i] 来推导，那么结果其实反而变小了，因为我们dp[i]要求的是最大和。所以在这种情况下，如果dp[i-1] < 0，那么dp[i]其实就是nums[i]的值。即

dp[i] = nums[i] , if (dp[i-1] < 0)

综上分析，我们可以得到：

dp[i]=max(nums[i], dp[i−1]+nums[i])

得到了状态转移方程，但是我们还需要通过一个已有的状态的进行推导，我们可以想到dp[0]一定是以nums[0]进行结尾，所以

dp[i] = dp[i-1]+nums[i] , if (dp[i-1] >= 0)
dp[0] = nums[0]

在很多题目中，因为dp[i]本身就定义成了题目中的问题，所以dp[i]最终就是要的答案。但是这里状态中的定义，并不是题目中要的问题，不能直接返回最后的一个状态 (这一步经常有初学者会摔跟头)。所以最终的答案，其实我们是寻找：

max(dp[0], dp[1], …, d[i-1], dp[i])

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        if len(nums) < 1:
            return 0
        dp = [nums[0]]
        if len(nums) == 1:
            return dp[0]
        for i in range(1, len(nums)):
            dp.append(max(nums[i], dp[i-1]+nums[i]))
        return max(dp)

执行耗时:44 ms,击败了90.97% 的Python3用户
内存消耗:14.2 MB,击败了24.24% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//Java
class Solution {
    public int maxSubArray(int[] nums) {
        if(nums.length < 1) return 0;
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int res = dp[0];
        for(int i=1; i<nums.length;i++){
            dp[i] = Math.max(dp[i-1]+nums[i], nums[i]);
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了94.84% 的用户
内存消耗：38.3 MB, 在所有 Java 提交中击败了76.68% 的用户

3.最长上升子序列

[第300题] 给定一个无序的整数数组，找到其中最长上升子序列的长度。

  • 示例:
    输入: [10,9,2,5,3,7,101,18]
    输出: 4
    解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

说明: 可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。

首先我们分析题目，要找的是最长上升子序列（Longest Increasing Subsequence，LIS）。因为题目中没有要求连续，所以LIS可能是连续的，也可能是非连续的。同时，LIS符合可以从其子问题的最优解来进行构建的条件。所以我们可以尝试用动态规划来进行求解。首先我们定义状态：

dp[i] ：表示以nums[i]结尾的最长上升子序列的长度

我们分两种情况进行讨论：

如果nums[i]比前面的所有元素都小，那么dp[i]等于1（即它本身）（该结论正确）

如果nums[i]前面存在比他小的元素，那么dp[i]就等于dp[i] = max(dp[j]+1，dp[k]+1，dp[p]+1，…..)
只要满足：
nums[i] > nums[j]
nums[i] > nums[k]
nums[i] > nums[p]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#Python
class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) < 1:
            return 0
        dp = [1]
        result = 1
        if len(nums) == 1:
            return result
        for i in range(1, len(nums)):
            dp.append(1)
            for j in range(i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[j]+1, dp[i])
            result = max(result, dp[i])
        return result

执行耗时:1344 ms,击败了26.36% 的Python3用户
内存消耗:13.6 MB,击败了5.92% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Java
class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        dp[0] = 1;
        int res = 1;
        for(int i=1; i<nums.length; i++){
            int maxLen = 1;
            for(int j=0; j<i; j++){
                if(nums[i] > nums[j]) maxLen = Math.max(maxLen, dp[j]+1);
            }
            dp[i] = maxLen;
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

执行用时：67 ms, 在所有 Java 提交中击败了75.12% 的用户
内存消耗：38.3 MB, 在所有 Java 提交中击败了15.62% 的用户

4.三角形最小路径和

[第120题] 给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。 相邻的结点在这里指的是下标与上一层结点下标相同或者等上一层结点下标 + 1的两个点。

  • 例如，给定三角形：
    1
    2
    3
    4
    5
    [	[2],     
       [3,4],    
      [6,5,7],   
     [4,1,8,3]
    ]
    自顶向下的最小路径和为11（即，2 + 3 + 5 + 1 = 11）。

我们根据题目中给出的条件：每一步只能移动到下一行中相邻的结点上。其实也就等同于，每一步我们只能往下移动一格或者右下移动一格。将其转化成代码，假如2所在的元素位置为[0,0]，那我们往下移动就只能移动到[1,0]或者[1,1]的位置上。假如5所在的位置为[2,1]，同样也只能移动到[3,1]和[3,2]的位置上。

所以我们通过动态规划进行求解。首先，我们定义状态：
dp[i][j] : 表示包含第i行j列元素的最小路径和
我们很容易想到可以自顶向下进行分析。并且，无论最后的路径是哪一条，它一定要经过最顶上的元
素，即[0,0]。所以我们需要对dp[0][0]进行初始化。
dp[0][0] = [0][0]位置所在的元素值
继续分析，如果我们要求dp[i][j]，那么其一定会从自己头顶上的两个元素移动而来。
得到状态转移方程：
dp[i][j] = min(dp[i-1][j-1],dp[i-1][j]) + triangle[i][j]
但是，我们这里会遇到一个问题！除了最顶上的元素之外，
最左边的元素只能从自己头顶而来
最右边的元素只能从自己左上角而来
然后，我们观察发现，位于第2行的元素，都是特殊元素（因为都只能从[0,0]的元素走过来）
我们可以直接将其特殊处理，得到：
dp[1][0] = triangle[1][0] + triangle[0][0]
dp[1][1] = triangle[1][1] + triangle[0][0]
最后，我们只要找到最后一行元素中，路径和最小的一个，就是我们的答案。即：
l：dp数组长度
result = min(dp[l-1,0]，dp[l-1,1]，dp[l-1,2]....)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#Python
class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        if len(triangle) < 1:
            return 0
        for i in range(1, len(triangle)):
            for j in range(len(triangle[i])):
                if j == 0:
                    triangle[i][j] = triangle[i - 1][j] + triangle[i][j]
                elif j == len(triangle[i]) - 1:
                    triangle[i][j] = triangle[i - 1][j - 1] + triangle[i][j]
                else:
                    triangle[i][j] = min(triangle[i - 1][j], triangle[i - 1][j - 1]) + triangle[i][j]
        return min(triangle[-1])

执行耗时:40 ms,击败了96.02% 的Python3用户
内存消耗:14 MB,击败了39.84% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Java
class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        if(n < 1) return 0;
        int[][] dp = new int[n][n];
        dp[0][0] = triangle.get(0).get(0);
        if(n < 2) return dp[0][0];
        int res = Integer.MAX_VALUE;
        for(int i = 1; i < n; i++){
            for(int j = 0; j < triangle.get(i).size(); j++){
                if(j == 0) dp[i][j] = triangle.get(i).get(j) + dp[i - 1][j];
                else if(j == triangle.get(i).size()-1){
                    dp[i][j] = triangle.get(i).get(j) + dp[i - 1][j-1];
                }else{
                    dp[i][j] = triangle.get(i).get(j) + Math.min(dp[i - 1][j], dp[i - 1][j - 1]);
                }
                if(i == n-1) res = Math.min(res, dp[i][j]);
            }
        }
        return res;
    }
}

执行用时：5 ms, 在所有 Java 提交中击败了21.88% 的用户
内存消耗：38.9 MB, 在所有 Java 提交中击败了5.22% 的用户

优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//Java
class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        //因为当前状态只与上一行的列有关，因此可以压缩空间
        //dp[j]代表第j列的最小路径和
        int[] dp = new int[n];
        dp[0] = triangle.get(0).get(0);
        for (int i = 1; i < n; ++i) {
            //更新最后一列
            dp[i] = dp[i - 1] + triangle.get(i).get(i);
            //更新中间列
            //需要逆序，否则上一列的值会被覆盖
            for (int j = i - 1; j > 0; --j) {
                dp[j] = Math.min(dp[j - 1], dp[j]) + triangle.get(i).get(j);
            }
            //更新第0列
            dp[0] += triangle.get(i).get(0);
        }
        int minTotal = dp[0];
        for (int i = 1; i < n; ++i) {
            minTotal = Math.min(minTotal, dp[i]);
        }
        return minTotal;
    }
}

执行用时：2 ms, 在所有 Java 提交中击败了94.30% 的用户
内存消耗：38.9 MB, 在所有 Java 提交中击败了5.22% 的用户

5.最小路径和

[第64题] 给定一个包含非负整数的m x n网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。 说明：每次只能向下或者向右移动一步。

  • 示例:
    输入:
    1
    2
    3
    4
    5
    [
    [1,3,1],
    [1,5,1],
    [4,2,1]
    ]
    输出: 7
    解释: 因为路径 1→3→1→1→1 的总和最小。

该题与上一道求三角形最小路径和一样，题目明显符合可以从子问题的最优解进行构建，所以我们考虑使用动态规划进行求解。首先，我们定义状态：
dp[i][j] : 表示包含第i行j列元素的最小路径和
同样，因为任何一条到达右下角的路径，都会经过[0,0]这个元素。所以我们需要对dp[0][0]进行初始化。
dp[0][0] = [0][0]位置所在的元素值
如果我们要求dp[i][j] ，那么它一定是从自己的上方或者左边移动而来
进而我们得到状态转移方程：
dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j]
同样我们需要考虑两种特殊情况：
最上面一行，只能由左边移动而来
最左边一列，只能由上面移动而来
最后，因为我们的目标是从左上角走到右下角，整个网格的最小路径和其实就是包含右下角元素的最小路径和。即：
最终结果就是：dp[l-1][len(dp[l-1])-1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#Python
class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        for i in range(len(grid)):
            for j in range(len(grid[i])):
                if (i == 0) and (j == 0):
                    grid[i][j] = grid[i][j]
                elif (i == 0) and (j != 0):
                    grid[i][j] = grid[i][j-1] + grid[i][j]
                elif (i != 0) and (j == 0):
                    grid[i][j] = grid[i-1][j] + grid[i][j]
                else:
                    grid[i][j] = min(grid[i][j-1], grid[i-1][j]) + grid[i][j]
        return grid[-1][-1]

执行耗时:72 ms,击败了19.09% 的Python3用户
内存消耗:14.8 MB,击败了23.49% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//Java
class Solution {
    public int minPathSum(int[][] grid) {
        for(int i=0; i < grid.length; i++){
            for(int j=0; j < grid[0].length; j++){
                if(i==0 && j==0) continue;
                else if(i==0 && j != 0) grid[i][j] = grid[i][j-1] + grid[i][j];
                else if(i!=0 && j == 0) grid[i][j] = grid[i-1][j] + grid[i][j];
                else grid[i][j] = Math.min(grid[i-1][j], grid[i][j-1]) + grid[i][j];
            }
        }
        return grid[grid.length-1][grid[0].length-1];
    }
}

执行用时：4 ms, 在所有 Java 提交中击败了15.82% 的用户
内存消耗：41 MB, 在所有 Java 提交中击败了86.60% 的用户

6.打家劫舍

[第198题] 你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

  • 示例 1：
    输入：[1,2,3,1]
    输出：4
    解释：偷窃1号房屋 (金额 = 1) ，然后偷窃3号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
  • 示例 2：
    输入：[2,7,9,3,1]#
    输出：12
    解释：偷窃1号房屋 (金额 = 2), 偷窃3号房屋 (金额 = 9)，接着偷窃5号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。

定义出状态:
dp[i] : 偷盗至第i个房子时，所获取的最大利益
因为小偷一定会从前偷到最后（强调：偷盗至第i个房间，不代表小偷要从第i个房间中获取财物）。所以我们的最终答案很容易确定。即：dp[i]
由于不可以在相邻的房屋闯入，所以至i房屋可盗窃的最大值，要么就是至i-1房屋可盗窃的最大值，要么就是至i-2房屋可盗窃的最大值加上当前房屋的值，二者之间取最大值，即：
dp[i] = max(dp[i-2]+nums[i], dp[i-1])

1
2
3
4
5
6
7
8
9
10
11
12
13
#Python
class Solution:
    def rob(self, nums: List[int]) -> int:
        if len(nums) < 1:
            return 0
        for i in range(len(nums)):
            if i == 0:
                nums[i] = nums[0]
            elif i == 1:
                nums[i] = max(nums[0], nums[1])
            else:
                nums[i] = max(nums[i-2]+nums[i], nums[i-1])
        return nums[-1]

执行耗时:32 ms,击败了96.55% 的Python3用户
内存消耗:13.5 MB,击败了5.36% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int rob(int[] nums) {
        if(nums.length < 1) return 0;
        int[] dp = new int[nums.length];
        for(int i=0; i<nums.length; i++){
            if(i==0) dp[0] = nums[0];
            else if(i==1) dp[1] = Math.max(nums[0], nums[1]);
            else dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]);
        }
        return dp[nums.length-1];
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.8 MB, 在所有 Java 提交中击败了61.62% 的用户

字符串系列

1.反转字符串

[第344题] 编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组char[]的形式给出。不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用O(1)的额外空间解决这一问题。你可以假设数组中的所有字符都是ASCII码表中的可打印字符。

  • 示例 1：
    输入：[“h”,”e”,”l”,”l”,”o”]
    输出：[“o”,”l”,”l”,”e”,”h”]
  • 示例 2：
    输入：[“H”,”a”,”n”,”n”,”a”,”h”]
    输出：[“h”,”a”,”n”,”n”,”a”,”H”]

这是一道相当简单的经典题目，直接上题解：使用双指针进行反转字符串。
假设输入字符串为[“h”,”e”,”l”,”l”,”0”]
定义left和right分别指向首元素和尾元素
当left < right ，进行交换。
交换完毕，left++，right—
直至left == right

1
2
3
4
5
6
7
8
9
10
11
12
#Python
class Solution:
    def reverseString(self, s: List[str]) -> None:
        """
        Do not return anything, modify s in-place instead.
        """
        left = 0
        right = len(s) - 1
        while left < right:
            s[left], s[right] = s[right], s[left]
            left += 1
            right -= 1

执行耗时:48 ms,击败了77.38% 的Python3用户
内存消耗:14.6 MB,击败了7.10% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Java
class Solution {
    public void reverseString(char[] s) {
        int left = 0;
        int right = s.length-1;
        while (left < right){
            swap(s, left, right);
            left++;
            right--;
        }
    }
    public void swap(char[] ch,int i,int j){
        char temp = ch[i];
        ch[i] = ch[j];
        ch[j] = temp;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：45.2 MB, 在所有 Java 提交中击败了33.90% 的用户

2.字符串中的第一个唯一字符

[第387题] 给定一个字符串，找到它的第一个不重复的字符，并返回它的索引。如果不存在，则返回 -1。

  • 示例：
    s = “leetcode” 返回 0
    s = “loveleetcode” 返回 2

提示：你可以假定该字符串只包含小写字母。

方法一：用字典

在数组中记录每个字母的最后一次出现的所在索引。然后再通过一次循环，比较各个字母第一次出现的索引是否为最后一次的索引。如果是，我们就找到了我们的目标，如果不是我们将其设为 -1（标示该元素非目标元素）如果第二次遍历最终没有找到目标，直接返回 -1即可。

1
2
3
4
5
6
7
8
9
10
11
12
#Python
class Solution:
    def firstUniqChar(self, s: str) -> int:
        dict = {}
        for i in range(len(s)):
            dict[s[i]] = i
        for i in range(len(s)):
            if i == dict[s[i]]:
                return i
            else:
                dict[s[i]] = -1
        return -1

执行耗时:128 ms,击败了61.83% 的Python3用户
内存消耗:13.7 MB,击败了5.07% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
//Java
class Solution {
    public int firstUniqChar(String s) {
        Map<Character, Integer> map = new HashMap<>();
        for(int i=0; i<s.length(); i++) map.put(s.charAt(i), i);
        for(int i=0; i<s.length(); i++){
            if (i == map.get(s.charAt(i))) return i;
            else map.put(s.charAt(i), -1);
        }
        return -1;
    }
}

执行用时：35 ms, 在所有 Java 提交中击败了27.69% 的用户
内存消耗：39.1 MB, 在所有 Java 提交中击败了27.58% 的用户

方法二：用集合

集合的特性为集合中每个元素都是独一无二的，我们可以利用这特性，将列表转换为集合。

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def firstUniqChar(self, s: str) -> int:
        # 转为集合, 将去重后的集合再转化为列表
        unique = list(set(s))
        # 按原列表索引排序，不改变顺序
        unique.sort(key=s.index)
        for i in unique:
            if s.count(i) == 1:
                return s.index(i)
        return -1

执行耗时:76 ms,击败了94.58% 的Python3用户
内存消耗:13.7 MB,击败了5.07% 的Python3用户

3.实现Sunday匹配

[第28题] 实现strStr()函数。给定一个haystack字符串和一个needle字符串，在haystack字符串中找出needle字符串出现的第一个位置 (从0开始)。如果不存在，则返回-1。

  • 示例 1:
    输入: haystack = “hello”, needle = “ll”
    输出: 2
  • 示例 2:
    输入: haystack = “aaaaa”, needle = “bba”
    输出: -1

说明:
当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当needle是空字符串时我们应当返回0 。这与C语言的strstr()以及Java的indexOf()定义相符。

先普及几个概念：

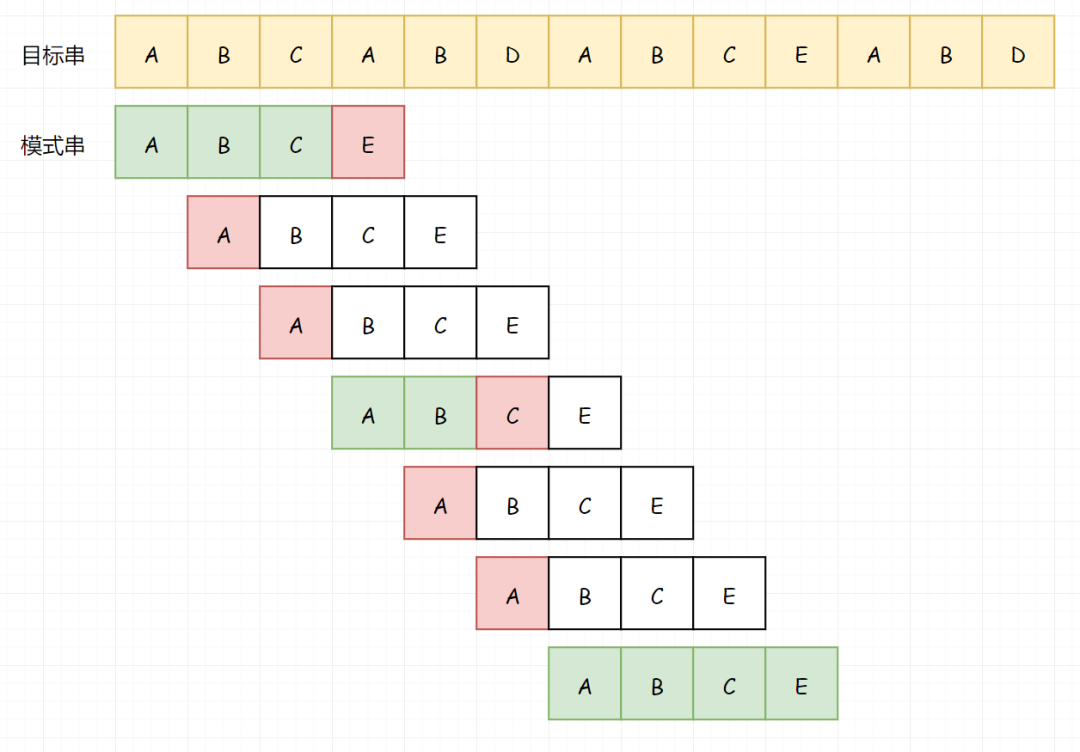
  • 串：串是字符串的简称
  • 空串：长度为零的串称为空串
  • 主串：包含子串的串相应地称为主串
  • 子串：串中任意个连续字符组成的子序列称为该串的子串
  • 模式串：子串的定位运算又称为串的模式匹配，是一种求子串第一个字符在主串中序号的运算。被匹配的主串称为目标串，子串称为模式串。

对于SUNDAY算法，我们从头部开始比较，一旦发现不匹配，直接找到主串中位于模式串后面的第一个字符，即下面绿色的 “s”。（因为，无论模式串移动多少步，模式串后的第一个字符都要参与下一次比较，也就是这里的 “s”）

找到了模式串后的第一个字符 “s”，接下来该怎么做？我们需要查看模式串中是否包含这个元素，如果不包含那就可以跳过一大片，从该字符的下一个字符开始比较。

因为仍然不匹配（空格和l），我们继续重复上面的过程。找到模式串的下一个元素：t

现在有意思了，我们发现t被包含于模式串中，并且t出现在模式串倒数第3个。所以我们把模式串向前移动3个单位：

捞干货，这个过程里我们做了一些什么：

  • 对齐目标串和模式串，从前向后匹配
  • 关注主串中位于模式串后面的第一个元素（核心）
  • 如果关注的字符没有在子串中出现则直接跳过
  • 否则开始移动模式串，移动位数 = 子串长度 - 该字符最右出现的位置(以0开始)

然而这种方法，我这里用Python写会超时，估计原因在于查找索引太耗时，还是用子串逐一比较来的实在img

1
2
3
4
5
6
7
8
#Python
class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        L, n = len(needle), len(haystack)
        for start in range(n - L + 1):
            if haystack[start: start + L] == needle:
                return start
        return -1

执行耗时:32 ms,击败了97.51% 的Python3用户
内存消耗:13.7 MB,击败了17.10% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
//Java
class Solution {
    public int strStr(String haystack, String needle) {
        if (haystack == null || needle == null) {
            return 0; 
        } 
        if (haystack.length() < needle.length()) {
            return -1; 
        }
        //目标串匹配索
        int originIndex = 0;
        //模式串匹配索引
        int aimIndex = 0;
        // 成功匹配完终止条件：所有needle均成功匹配
        while (aimIndex < needle.length()) {
            // 针对origin匹配完，但needle未匹配完情况处理
            if (originIndex > haystack.length() - 1) return -1;
            if (haystack.charAt(originIndex) == needle.charAt(aimIndex)) {
                // 匹配则index均加1
                originIndex++;
                aimIndex++;
            } else {
                //下一个目标字符索引
                int nextCharIndex = originIndex - aimIndex + needle.length();
                //判断下一个目标字符（图里的那个绿框框）是否存在。
                if (nextCharIndex < haystack.length()) {
                    // 判断目标字符在模式串中匹配到，返回最后一个匹配的index
                    int step = needle.lastIndexOf(haystack.charAt(nextCharIndex));
                    if (step == -1) {
                        // 不存在的话，设置到目标字符的下一个元素
                        originIndex = nextCharIndex + 1;
                    } else {
                        // 存在的话，移动对应的数字（参考上文中的存在公式）
                        originIndex = nextCharIndex - step;
                    }
                    //模式串总是从第一个开始匹配
                    aimIndex = 0;
                } else {
                    return -1;
                }
            }
        }
        return originIndex - aimIndex;
    }
}

执行用时：4 ms, 在所有 Java 提交中击败了28.87% 的用户
内存消耗：37 MB, 在所有 Java 提交中击败了68.02% 的用户

4.大数打印

剑指offer 17：大数打印
输入数字n，按顺序打印出从1到最大的n位十进制数。比如输入3，则打印出 1、2、3 一直到最大的3位数 999。

示例 1:

1
2
输入: n = 1 
输出: [1,2,3,4,5,6,7,8,9]

说明：

  • 用返回一个整数列表来代替打印
  • n 为正整数

题目升级： 这道题目的名字叫做大数打印，如果阈值超出long类型，该怎么办呢？请手动实现一下！

采用数组进行存储。

  • 对最低位nSum的值递增（也就是字符串加1运算），当大于等于10时，我们把进位标识改为1，同时恢复对nSum减10（29-31）
  • 通过判断首位是否进位来判断到达最大的n位数情况。比如n=4，只有对9999加1，才会对第一个字符进位。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#Python
class Solution:
    def printNumbers(self, n: int) -> List[int]:
        result = []
        num = [0 for _ in range(n)]
        isBegin = True
        while isBegin:
            # tmp用于存储进位，初始值为1代表加1
            tmp = 1
            for i in range(len(num)-1, -1, -1):
                # python divmod() 函数把除数和余数运算结果结合起来，返回一个包含商和余数的元组(a // b, a % b)。
                tmp, num[i] = divmod(num[i] + tmp, 10)
                if tmp > 0 and i != 0:
                    continue
                elif tmp == 0:
                    break
                else:
                    # 直到最后一位仍进位就结束
                    isBegin = False
            if isBegin:
                result.append(int(''.join(map(str, num))))
        return result

执行用时：200 ms, 在所有 Python3 提交中击败了5.22% 的用户
内存消耗：20.3 MB, 在所有 Python3 提交中击败了18.63% 的用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//Java
class Solution {
    public int[] printNumbers(int n) {
        int max = (int)Math.pow(10, n)-1;
        int[] res = new int[max];
        char[] num  = new char[n];
        Arrays.fill(num, '0');
        boolean isBegin = true;
        int index = 0;
        while(isBegin){
            int tmp = 1;
            for(int i =n-1; i>=0; i--){
                int sum = num[i] - '0' + tmp;
                num[i] = (char) (sum % 10 + '0');
                tmp = sum / 10;
                if(tmp > 0 && i != 0) continue;
                else if(tmp == 0) break;
                else isBegin = false;
            }
            if(isBegin) res[index++] = saveNumber(num);
        }
        return res;

    }
    public int saveNumber(char[] number) {
        String res = "";
        boolean isBegin = false;
        for (char c : number) {
            if (!isBegin && c != '0') isBegin = true;
            if (isBegin) res += c;
        }
        return Integer.valueOf(res);
    }
}

执行用时：60 ms, 在所有 Java 提交中击败了5.31% 的用户
内存消耗：46.3 MB, 在所有 Java 提交中击败了91.10% 的用户

5.验证回文串

第125题：验证回文串
给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。

说明： 本题中，我们将空字符串定义为有效的回文串。

示例 1:

1
2
输入: "A man, a plan, a canal: Panama"
输出: true

示例 2:

1
2
输入: "race a car"
输出: false

“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。

当然，对于本题而言，因为原字符串还包括了除字母，数字之外的一些幺蛾子，所以我们可以考虑将其替换或跳过。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#Python
class Solution:
    def isPalindrome(self, s: str) -> bool:
        # 转换成小写
        s = s.lower()
        # 两头遍历比对
        i = 0
        j = len(s) - 1
        while i < j:
        	# 跳过特殊符号
            if not ((s[i] >= '0' and s[i] <= '9') or (s[i] >= 'a' and s[i] <= 'z')):
                i += 1
                continue
            if not ((s[j] >= '0' and s[j] <= '9') or (s[j] >= 'a' and s[j] <= 'z')):
                j -= 1
                continue
            if s[i] != s[j]:
                return False
            i += 1
            j -= 1
        return True

执行耗时:60 ms,击败了61.53% 的Python3用户
内存消耗:13.8 MB,击败了53.68% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//Java
class Solution {
    public boolean isPalindrome(String s) {
        String str = s.toLowerCase();
        int l = 0;
        int r = str.length()-1;
        while(l < r){
            if (!((str.charAt(l) >= '0' && str.charAt(l) <= '9') || (str.charAt(l) >= 'a' && str.charAt(l) <= 'z'))){
                l++;
                continue;
            }
            if (!((str.charAt(r) >= '0' && str.charAt(r) <= '9') || (str.charAt(r) >= 'a' && str.charAt(r) <= 'z'))){
                r--;
                continue;
            }
            if(str.charAt(l) != str.charAt(r)) return false;
            l++;
            r--;
        }
        return true;
    }
}

执行用时：4 ms, 在所有 Java 提交中击败了64.94% 的用户
内存消耗：38.4 MB, 在所有 Java 提交中击败了73.12% 的用户

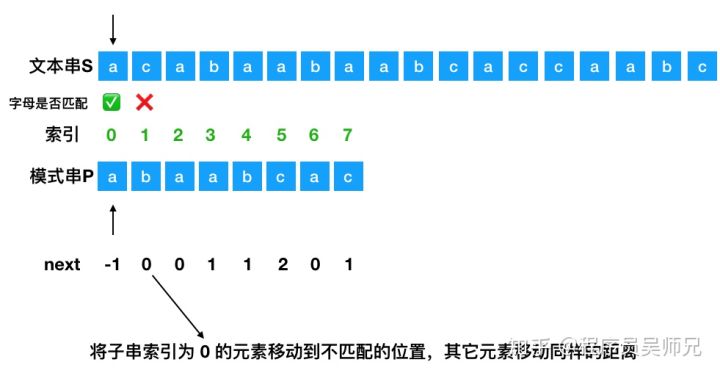
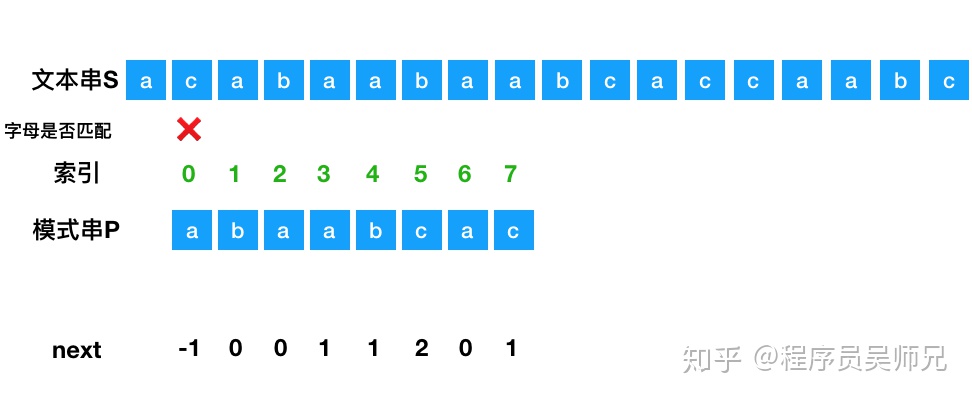
6.KMP

KMP 算法常被称为“看毛片算法”，由一个姓K的，一个姓M的，一个姓P 一起提出。是一种由暴力匹配改进的字符串匹配算法。

暴力匹配，就是目标串和模式串一个一个的对比。假若我们目标串长度为m，模式串长度为n。模式串与目标串至少比较m次，又因其自身长度为n，所以理论的时间复杂度为O(m*n)。 但因为途中遇到不能匹配的字符时，就可以停止，并不需要完全对比（比如上图第2行）。所以虽然理论时间复杂度为 O(m*n) ，但其实大部分情况效率高很多。

下面直接给出 KMP算法 的操作流程：

  • 假设现在文本串 S 匹配到 i 位置，模式串 P 匹配到 j 位置
  • 如果 j = -1，或者当前字符匹配成功（即 S[i] == P[j] ），都令 i++，j++，继续匹配下一个字符； 如果 j != -1，且当前字符匹配失败（即 S[i] != P[j] ），则令 i 不变，j = next[j]。此举意味着失配时，模式串 P相对于文本串 S 向右移动了 j - next [j] 位
  • 换言之，将模式串 P 失配位置的 next 数组的值对应的模式串 P 的索引位置移动到失配处

以下图文本串 S 与模式串 P 为例：


求得每一个子串的所有前缀与后缀。
前缀指除了最后一个字符以外，一个字符串的全部头部组合；后缀指除了第一个字符以外，一个字符串的全部尾部组合。

求得原模式串 P 的子串对应的各个前缀后缀的公共元素的最大长度表下图。

根据最大长度表去求next数组：next数组相当于“最大长度值” 整体向右移动一位，然后初始值赋为-1。

好了，获取了next 数组后，KMP 算法的操作就很清晰了。

将模式串 P 与文本串 S 的字母一个个进行匹配，当失配的时候，模式串向右移动。比如模式串的 b 与文本串的 c 失配了，找出失配处模式串的next数组里面对应的值，这里为 0，然后将索引为 0 的位置移动到失配处。

例子：



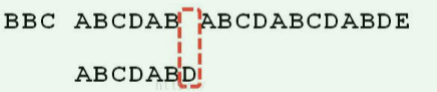
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//Java
import java.util.Arrays;

public class KMPAlgorithm {
    public static void main(String[] args) {
        String str1 = "BBC ABCDAB ABCDABCDABDE";
        String str2 = "ABCDABD";
        //得到目标子串的部分匹配值
        int[] next = kmpNext(str2);
        System.out.println("next="+ Arrays.toString(next));

        int index = kmpSearch(str1, str2, next);
        System.out.println("index= " +index);
    }
    /**
     *
     * @param str1 源字符串
     * @param str2 子串
     * @param next 部分匹配表，是子串对应的部分匹配表
     * @return 如果是-1就是没有匹配到，否则返回第一个匹配的位置
     */
    public static int kmpSearch(String str1, String str2, int[] next){
        //遍历
        for (int i=0, j=0; i< str1.length(); i++) {
            //若匹配不成功，目标子串偏移, 移动位数为（已匹配字符数-部分匹配值）相当于next右移
            //因此j = j - next[j-1]或j = next[j-1]都可
            if (j > 0 && str1.charAt(i) != str2.charAt(j)) j= next[j-1];
            //记录已匹配的字符数
            if (str1.charAt(i) == str2.charAt(j)) j++;
            //匹配成功, 返回索引
            if (j == str2.length()) return i-j+1;
        }
        //匹配不成功，返回-1
        return -1;
    }

    //获取到一个字符串（子串）的部分匹配值表
    public  static int[] kmpNext(String dest){
        //创建一个next数组保存部分匹配值
        int[] next = new int[dest.length()];
        next[0] = 0;//如果字符串是长度为1部分匹配值就是0
        // i相当于后缀，一步步遍历目标串的子串, j代表公共前缀长
        for (int i=1, j=0; i< dest.length(); i++){
            //若后缀不等于前缀，则公共前缀长归0
            if (j > 0 && dest.charAt(i) != dest.charAt(j)) j = 0;
            //随着后缀长度增加 若后缀一直等于前缀，公共前缀长+1
            if (dest.charAt(i) == dest.charAt(j)) j++;
            //部分匹配值为公共前缀长
            next[i] = j;
        }
        return next;
    }
}

7.旋转字符串

第796题：旋转字符串
给定两个字符串, A 和 B。A 的旋转操作就是将 A 最左边的字符移动到最右边。例如, 若 A = ‘abcde’，在移动一次之后结果就是’bcdea’ 。如果在若干次旋转操作之后，A 能变成B，那么返回True。

示例 1:

1
2
输入: A = 'abcde', B = 'cdeab'
输出: true

示例 2:

1
2
输入: A = 'abcde', B = 'abced'
输出: false

注意： A 和 B 长度不超过 100。

无论它怎样旋转，最终的 A + A包含了所有可以通过旋转操作从 A 得到的字符串：

那我们只需要判断 B 是否为 A + A 的子串就可以了。

1
2
3
4
#Python
class Solution:
    def rotateString(self, A: str, B: str) -> bool:
        return len(A) == len(B) and (B in (A + A))

执行耗时:44 ms,击败了35.30% 的Python3用户
内存消耗:13.4 MB,击败了48.35% 的Python3用户

1
2
3
4
5
6
7
//Java
class Solution {
    public boolean rotateString(String A, String B) {
        String s = A + A;
        return A.length()==B.length() && s.contains(B)?true: false;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.5 MB, 在所有 Java 提交中击败了37.20% 的用户

8.最后一个单词的长度

第58题：最后一个单词的长度
给定一个仅包含大小写字母和空格 ‘ ‘ 的字符串 s，返回其最后一个单词的长度。如果字符串从左向右滚动显示，那么最后一个单词就是最后出现的单词。

示例：

1
2
输入: "Hello World" 
输出: 5

说明： 一个单词是指仅由字母组成、不包含任何空格字符的 最大子字符串。

题中的陷阱在于，结尾处仍然可能有空格。

所以一般的解题思路为，先去掉末尾的空格，然后从尾向前开始遍历，直到遇到第一个空格处结束。

1
2
3
4
5
#Python
class Solution:
    def lengthOfLastWord(self, s: str) -> int:
        # 去除字符串开头或者结尾的空格,再按空格划分
        return len(s.strip().split(' ')[-1])

执行耗时:32 ms,击败了94.69% 的Python3用户
内存消耗:13.6 MB,击败了12.63% 的Python3用户

1
2
3
4
5
6
7
//Java
class Solution {
    public int lengthOfLastWord(String s) {
        String[] str = s.trim().split(" ");
        return str[str.length-1].length();
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了38.46% 的用户
内存消耗：37.2 MB, 在所有 Java 提交中击败了8.91% 的用户

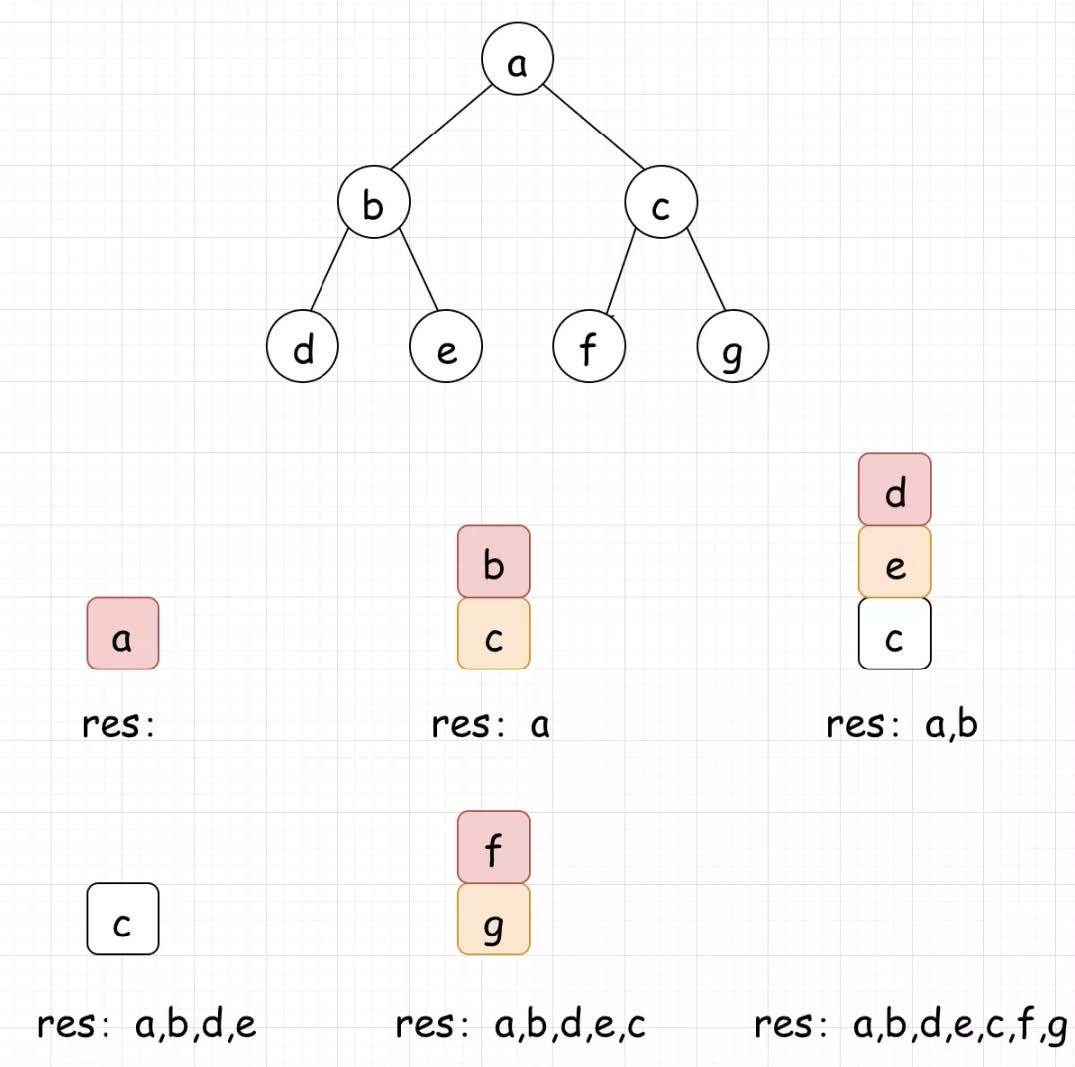
二叉树系列

1.最大深度与DFS

在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。树比链表稍微复杂，因为链表是线性数据结构，而树不是。树的问题很多都可以由广度优先搜索或深度优先搜索解决。

[第104题] 给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。说明: 叶子节点是指没有子节点的节点。

  • 示例：
    1
    2
    3
    4
    5
    6
    给定二叉树 [3,9,20,null,null,15,7]，
        3
       / \
      9  20
         / \
        15  7
    返回它的最大深度 3 。

方法一：递归求解

每个节点的深度与它左右子树的深度有关，且等于其左右子树最大深度值加上1，即
maxDepth(root) = max(maxDepth(root.left), maxDepth(root.right)) + 1

1
2
3
4
5
6
#Python
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

执行耗时:56 ms,击败了54.54% 的Python3用户
内存消耗:15.4 MB,击败了12.04% 的Python3用户

1
2
3
4
5
6
7
//Java
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.6 MB, 在所有 Java 提交中击败了12.93% 的用户

方法二：非递归DFS

DFS：深度优先搜索算法（Depth First Search），对于二叉树而言，它沿着树的深度遍历树的节点，尽可能深的搜索树的分支，这一过程一直进行到已发现从源节点可达的所有节点为止。
如下图二叉树，它的访问顺序为：A-B-D-E-C-F-G

1
2
3
4
5
    a
   / \
  b    c
 / \  / \
d   e f  g

虽然我们用递归的方式根据DFS的思想顺利完成了题目。但是这种方式的缺点却显而易见。因为在递归中，如果层级过深，我们很可能保存过多的临时变量，导致栈溢出。这也是为什么我们一般不在后台代码中使用递归的原因。
事实上，函数调用的参数是通过栈空间来传递的，在调用过程中会占用线程的栈资源。而递归调用，只有走到最后的结束点后函数才能依次退出，而未到达最后的结束点之前，占用的栈空间一直没有释放，如果递归调用次数过多，就可能导致占用的栈资源超过线程的最大值，从而导致栈溢出，导致程序的异常退出。
如何将递归的代码转化成非递归的形式。这里请记住，99%的递归转非递归，都可以通过栈来进行实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#Python
class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        #stack记录的是节点
        #是同时入栈同时出栈，level记录的是节点在第几层
        stack = []
        level = [1]
        maxdepth = 0
        stack.append(root)
        while stack:
            #stack中的元素和level中的元素同时出栈
            node = stack.pop()
            temp = level.pop()
            maxdepth = max(temp, maxdepth)
            if node.right:
                # 同时入栈
                stack.append(node.right)
                level.append(temp + 1)
            if node.left:
                # 同时入栈
                stack.append(node.left)
                level.append(temp + 1)

        return maxdepth

执行耗时:44 ms,击败了97.17% 的Python3用户
内存消耗:14.6 MB,击败了81.81% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//Java
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        Stack<TreeNode> stack = new Stack<>();
        Stack<Integer> level = new Stack<>();
        int maxdepth = 0;
        stack.push(root);
        level.push(1);
        while(!stack.empty()){
            TreeNode node = stack.pop();
            int tmp = level.pop();
            maxdepth = Math.max(maxdepth, tmp);
            if(node.right!=null){
                stack.push(node.right);
                level.push(tmp+1);
            }
            if(node.left!=null){
                stack.push(node.left);
                level.push(tmp+1);
            }
        }
        return maxdepth;
    }
}

执行用时：3 ms, 在所有 Java 提交中击败了16.83% 的用户
内存消耗：38.1 MB, 在所有 Java 提交中击败了94.17% 的用户

如果不理解代码，请看下图：

1：首先将a压入栈
2：a弹栈，将c、b压入栈（注意顺序）
3：b弹栈，将e、d压入栈
4：d、e、c弹栈，将g、f压入栈
5：f、g弹栈

唯一需要强调的是，为什么需要先右后左压入数据？是因为我们需要将先访问的数据，后压入栈（请思考栈的特点）。

2.层次遍历与BFS

在上一节中，我们通过例题学习了二叉树的DFS（深度优先搜索），其实就是沿着一个方向一直
向下遍历。那我们可不可以按照高度一层一层的访问树中的数据呢？当然可以，就是本节中我们
要讲的BFS（宽度优先搜索），同时也被称为广度优先搜索。

其实就是从上到下，先把每一层遍历完之后再遍历一下一层。假如我们的树如下：

1
2
3
4
5
    a
   / \
  b    c
 / \  / \
d   e f  g

按照BFS，访问顺序如下：
a->b->c->d->e->f->g

[第102题] 给你一个二叉树，请你返回其按层序遍历得到的节点值。（即逐层地，从左到右访问所有节点）。

  • 示例：
    二叉树：[3,9,20,null,null,15,7]
    1
    2
    3
    4
    5
      3
     / \
    9  20
      /  \
     15   7
    返回其层次遍历结果：
    1
    2
    3
    4
    5
    [
      [3],
      [9,20],
      [15,7]
    ]

方法一：DFS递归求解

想到递归，我们一般先想到DFS。我们可以对该二叉树进行先序遍历（根左右的顺序），同时，记录节点所在的层次level，并且对每一层都定义一个数组，然后将访问到的节点值放入对应层的数组中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#Python
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        self.result = []
        self._dfs(root, 0)
        return self.result

    def _dfs(self, node, level):
        if not node:
            return
        if len(self.result) < level + 1:
            self.result.append([])
        self.result[level].append(node.val)
        self._dfs(node.left, level + 1)
        self._dfs(node.right, level + 1)

执行耗时:36 ms,击败了94.65% 的Python3用户
内存消耗:14 MB,击败了11.12% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
     public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList();
        levelOrder(root, result, 0);
        return result;
    }

    public void levelOrder(TreeNode root, List<List<Integer>> result, int level) {
        if (root == null) return;
        while (result.size() < level + 1) {
            List<Integer> item = new ArrayList();
            result.add(item);
        }
        result.get(level).add(root.val);
        levelOrder(root.left, result, level + 1);
        levelOrder(root.right, result, level + 1);
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.8 MB, 在所有 Java 提交中击败了14.02% 的用户

方法二：BFS求解

上面的解法，其实相当于是用DFS的方法实现了二叉树的BFS。那我们能不能直接使用BFS的方式进行解题呢？当然，我们可以使用Queue的数据结构。我们将root节点初始化进队列，通过消耗尾部，插入头部的方式来完成BFS。

具体步骤如下图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#Python
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        result = []
        # 初始化队列
        queue = collections.deque()
        queue.append(root)
        while queue:
            current_level = []
            # 同一层从右进，从左出
            for _ in range(len(queue)):
                node = queue.popleft()
                current_level.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            # 添加每层的节点
            result.append(current_level)
        return result

执行耗时:40 ms,击败了84.08% 的Python3用户
内存消耗:13.7 MB,击败了32.49% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//Java
class Solution {
     public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root==null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            List<Integer> tmp = new ArrayList<>();
            int size = queue.size();
            for(int i =0; i<size; i++) {
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if(node.left!=null) queue.offer(node.left);
                if(node.right!=null) queue.offer(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了94.76% 的用户
内存消耗：38.6 MB, 在所有 Java 提交中击败了68.05% 的用户

3.BST与其验证

先看定义：二叉搜索树（Binary Search Tree），（又：二叉查找树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉搜索树。

这里强调一下子树的概念：设T是有根树，a是T中的一个顶点，由a以及a的所有后裔（后代）导出的子图称为有向树T的子树。具体来说，子树就是树的其中一个节点以及其下面的所有的节点所构成的树。

比如下面这就是一颗二叉搜索树：

下面这两个都不是：

<1>图中4节点位置的数值应该大于根节点

<2>图中3节点位置的数值应该大于根节点

[第98题] 给定一个二叉树，判断其是否是一个有效的二叉搜索树。假设一个二叉搜索树具有如下特征：节点的左子树只包含小于当前节点的数。节点的右子树只包含大于当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。

  • 示例 1:
    输入:
    1
    2
    3
      2
     / \
    1   3
    输出: true
  • 示例 2:
    输入:
    1
    2
    3
    4
    5
      5
     / \
    1   4
       / \
         3   6
    输出: false
    解释: 输入为: [5,1,4,null,null,3,6]。根节点的值为 5 ，但是其右子节点值为 4 。

首先看完题目，我们很容易想到遍历整棵树，比较所有节点，通过左节点值<节点值，右节点值>节点值的方式来进行求解。但是这种解法是错误的，因为对于任意一个节点，我们不光需要左节点值小于该节点，并且左子树上的所有节点值都需要小于该节点。（右节点一致）所以我们在此引入上界与下界，用以保存之前的节点中出现的最大值与最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
#Python
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        if not root:
            return True
        return self.isBST(root, -inf, inf)

    def isBST(self, root, min, max):
        if not root:
            return True
        if (min >= root.val) or (max <= root.val):
            return False
        return self.isBST(root.left, min, root.val) and self.isBST(root.right, root.val, max)

执行耗时:52 ms,击败了88.67% 的Python3用户
内存消耗:15.8 MB,击败了38.48% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
//Java
class Solution {
    public boolean isValidBST(TreeNode root) {
        return isBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }
    public boolean isBST(TreeNode root, long min, long max){
        if(root==null) return true;
        if(root.val <= min || root.val >= max) return false;
        return isBST(root.left, min, root.val) && isBST(root.right, root.val, max);
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.4 MB, 在所有 Java 提交中击败了7.36% 的用户

4.BST的查找

[第700题] 给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

  • 例如，
    给定二叉搜索树:
    1
    2
    3
    4
    5
        4
       / \
      2   7
     / \
    1   3
    和值: 2
    你应该返回如下子树:
    1
    2
    3
      2     
     / \   
    1   3
    在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

假设目标值为 val，根据BST的特性，我们可以很容易想到查找过程
如果val小于当前结点的值，转向其左子树继续搜索；
如果val大于当前结点的值，转向其右子树继续搜索；
如果已找到，则返回当前结点。

方法一：递归

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        if not root:
            return
        if root.val > val:
            return self.searchBST(root.left, val)
        elif root.val < val:
            return self.searchBST(root.right, val)
        else:
            return root

执行耗时:116 ms,击败了10.76% 的Python3用户
内存消耗:15.5 MB,击败了33.59% 的Python3用户

1
2
3
4
5
6
7
8
9
//Java
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root==null) return null;
        if(root.val > val) return searchBST(root.left, val);
        else if(root.val < val) return searchBST(root.right, val);
        else return root;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：39.2 MB, 在所有 Java 提交中击败了83.28% 的用户

方法二：迭代

递归与迭代的区别
递归：重复调用函数自身实现循环称为递归；
迭代：利用变量的原值推出新值称为迭代，或者说迭代是函数内某段代码实现循环；

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        while root:
            if root.val > val:
                root = root.left
            elif root.val < val:
                root = root.right
            else:
                return root
        return

执行耗时:76 ms,击败了99.39% 的Python3用户
内存消耗:15.6 MB,击败了6.14% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
//Java
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        while(root!=null){
            if(root.val > val) root = root.left;
            else if(root.val < val) root = root.right;
            else return root;
        }
        return null;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：39.6 MB, 在所有 Java 提交中击败了8.04% 的用户

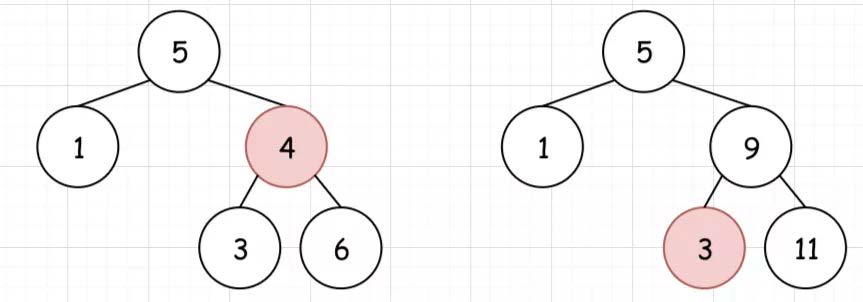
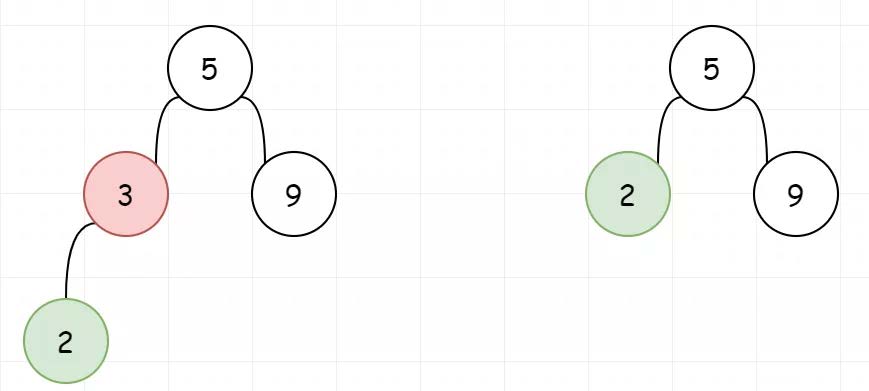
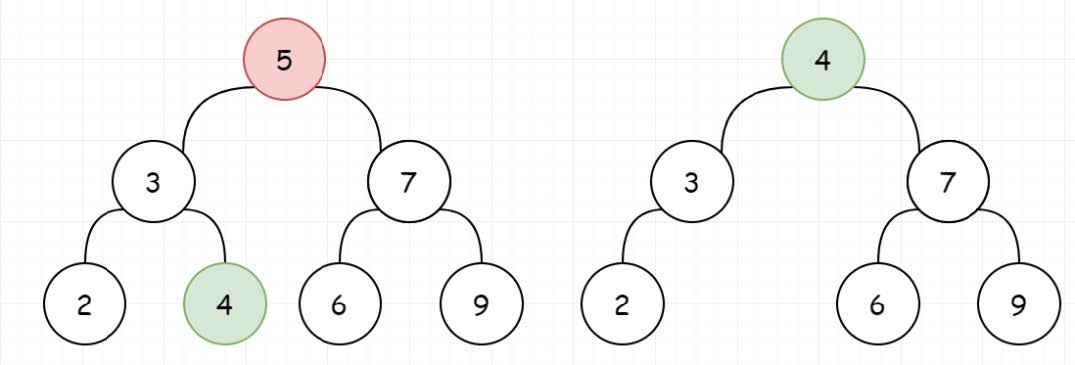
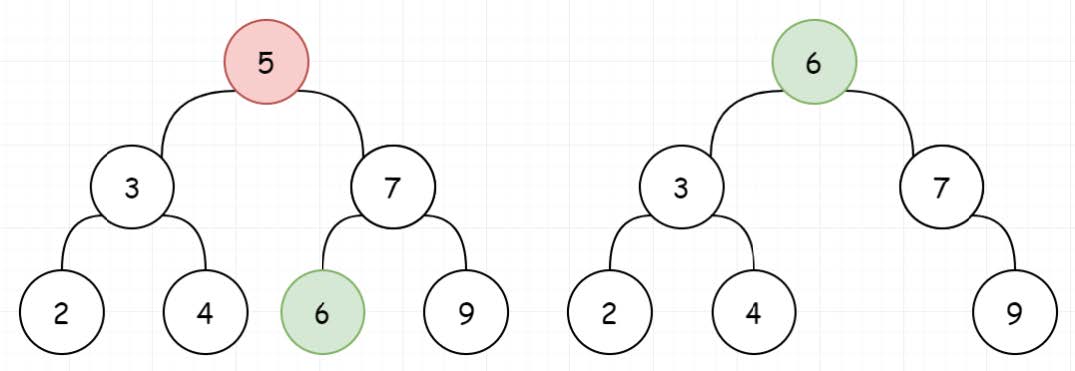
5.BST的删除

[第450题] 给定一个二叉搜索树的根节点root和一个值key，删除二叉搜索树中的key对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。一般来说，删除节点可分为两个步骤：首先找到需要删除的节点；如果找到了，删除它。
说明： 要求算法时间复杂度为O(h)，h为树的高度。

  • 示例:
    root = [5,3,6,2,4,null,7]
    key = 3
    1
    2
    3
    4
    5
        5
       / \
      3   6
     / \   \
    2   4   7
    给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
    一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
    1
    2
    3
    4
    5
        5
       / \
      4   6
     /     \
    2       7
    另一个正确答案是 [5,2,6,null,4,null,7]。
    1
    2
    3
    4
    5
      5
     / \
    2   6
     \   \
      4   7

我们要删除BST的一个节点，首先需要找到该节点。而找到之后，会出现三种情况。

1、待删除的节点左子树为空，让待删除节点的右子树替代自己。

2、待删除的节点右子树为空，让待删除节点的左子树替代自己。

3、如果待删除的节点的左右子树都不为空。我们需要找到比当前节点小的最大节点（前驱），来替换自己

或者比当前节点大的最小节点（后继），来替换自己。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#Python
class Solution:
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return None
        if root.val > key:
            root.left = self.deleteNode(root.left, key)
        elif root.val < key:
            root.right = self.deleteNode(root.right, key)
        else:
            #第一种和第二种情况
            if not root.left or not root.right:
                root = root.left if root.left else root.right
            else:
                # 第三种情况，查找后继
                cur = root.right
                while cur.left:
                    cur = cur.left
                root.val = cur.val
                # 找到右子树最小值，再通过主递归函数删除最小值
                # 出口就是 if not root.left or not root.right: root = root.left if root.left else root.right
                root.right = self.deleteNode(root.right, cur.val)

        return root

执行耗时:72 ms,击败了99.85% 的Python3用户
内存消耗:17.6 MB,击败了24.40% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//Java
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null) return null;
        if(root.val > key) root.left = deleteNode(root.left, key);
        else if(root.val < key) root.right = deleteNode(root.right, key);
        else{
            if(root.left==null || root.right==null ){
                root = root.left!=null?root.left: root.right;
            }
            else{
                TreeNode cur = root.right;
                while(cur.left!=null) cur = cur.left;
                root.val = cur.val;
                root.right = deleteNode(root.right, cur.val);
            }
        }
        return root;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.9 MB, 在所有 Java 提交中击败了62.43% 的用户

6.平衡二叉树

[第110题] 给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

  • 示例 1:
    给定二叉树 [3,9,20,null,null,15,7]
    1
    2
    3
    4
    5
      3
     / \
    9  20
      /  \
     15   7
    返回 true 。
  • 示例 2:
    给定二叉树 [1,2,2,3,3,null,null,4,4]
    1
    2
    3
    4
    5
    6
    7
          1
         / \
        2   2
       / \
      3   3
     / \
    4   4
    返回 false 。

我们想判断一棵树是否满足平衡二叉树，无非就是判断当前结点的两个孩子是否满足平衡，同时两个孩子的高度差是否超过1。那只要我们可以得到高度，再基于高度进行判断即可。

这里唯一要注意的是，当我们判定其中任意一个节点如果不满足平衡二叉树时，那说明整棵树已经不是一颗平衡二叉树，我们可以对其进行阻断，不需要继续递归下去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Python
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if not root:
            return True
        # 不平衡的情况有3种：左树不平衡、右树不平衡、左树和右树差的绝对值大于1
        if not self.isBalanced(root.left) or not self.isBalanced(root.right):
            return False
        leftH = self.maxDepth(root.left) + 1
        rightH = self.maxDepth(root.right) + 1
        if abs(leftH - rightH) > 1:
            return False
        return True

    def maxDepth(self, root):
        if not root:
            return 0
        # 树的深度为左右俩子树最大深度 + 1
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

执行耗时:64 ms,击败了73.12% 的Python3用户
内存消耗:17.3 MB,击败了66.69% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//Java
class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        else if(!isBalanced(root.left) || !isBalanced(root.right)) return false;
        else{
            int leftH = maxDepth(root.left) + 1;
            int rightH = maxDepth(root.right) + 1;
            if(Math.abs(leftH - rightH) > 1) return false;
            else return true;
        }
    }

    public int maxDepth(TreeNode root){
        if(root == null) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了99.97% 的用户
内存消耗：39.2 MB, 在所有 Java 提交中击败了5.03% 的用户

7.完全二叉树

如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。（二叉树的度代表某个结点的孩子或者说直接后继的个数。对于二叉树而言，1度是只有一个孩子或者说单子树,2度是有两个孩子或者说左右子树都有。）

满二叉树如下：


如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为
完全二叉树。

比如下面这颗：


而这颗就不是：

[第222题] 给出一个完全二叉树，求出该树的节点个数。
说明：
完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第h层，则该层包含1~ 2h个节点。

  • 示例:
    输入:
    1
    2
    3
    4
    5
        1
       / \
      2   3
     / \  /
    4  5 6
    输出: 6

方法一：递归求解

1
2
3
4
5
6
#Python
class Solution:
    def countNodes(self, root: TreeNode) -> int:
        if not root:
            return 0
        return 1 + self.countNodes(root.left) + self.countNodes(root.right)

执行耗时:88 ms,击败了91.26% 的Python3用户
内存消耗:20.5 MB,击败了6.22% 的Python3用户

但是很明显，出题者肯定不是要这种答案。因为这种答案和完全二叉树一毛钱关系都没有。所以我们继
续思考。

1
2
3
4
5
6
7
//Java
class Solution {
    public int countNodes(TreeNode root) {
        if(root == null) return 0;
        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：41.1 MB, 在所有 Java 提交中击败了23.37% 的用户

方法二：经典解法

由于题中已经告诉我们这是一颗完全二叉树，我们又已知了完全二叉树除了最后一层，其他层都是满的，并且最后一层的节点全部靠向了左边。那我们可以想到，可以将该完全二叉树可以分割成若干满二叉树和完全二叉树，满二叉树直接根据层高h计算出节点为2^h-1，然后继续计算子树中完全二叉树节点。那如何分割成若干满二叉树和完全二叉树呢？对任意一个子树，遍历其左子树层高left，右子树层高right，相等左子树则是满二叉树，否则右子树是满二叉树。

如下：


左子树为满二叉树

右子树为满二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#Python
class Solution:
    def countNodes(self, root: TreeNode) -> int:
        if not root:
            return 0
        # 计算左右子树高度
        lh, rh = self.__getHeight(root.left), self.__getHeight(root.right)
        if lh == rh:  # 左右子树高度相同，说明左子树必满 则节点数=左子树节点 + root节点(=1) + 递归找右子树
            return (pow(2, lh) - 1) + 1 + self.countNodes(root.right)
        else:  # 左子树比右子树高，说明右子树必满 同理
            return (pow(2, rh) - 1) + 1 + self.countNodes(root.left)

    def __getHeight(self, root):
        level = 0
        while root:
            level += 1
            root = root.left
        return level

执行耗时:88 ms,击败了91.26% 的Python3用户
内存消耗:20.4 MB,击败了47.22% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
    public int countNodes(TreeNode root) {
        if(root == null) return 0;
        int lh = getHeight(root.left);
        int rh = getHeight(root.right);
        if(lh == rh) return (int)(Math.pow(2, lh) - 1) + 1 + countNodes(root.right);
        else return (int)(Math.pow(2, rh) - 1) + 1 + countNodes(root.left);
    }

    public int getHeight(TreeNode root){
        int level = 0;
        while(root != null){
            level++;
            root = root.left;
        }
        return level;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：41 MB, 在所有 Java 提交中击败了50.61% 的用户

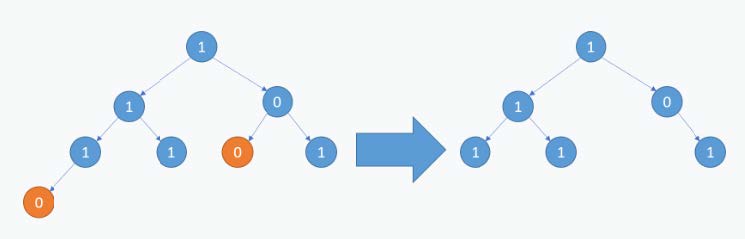
8.二叉树的剪枝

假设有一棵树，最上层的是root节点，而父节点会依赖子节点。如果现在有一些节点已经标记为无效，我们要删除这些无效节点。如果无效节点的依赖的节点还有效，那么不应该删除，如果无效节点和它的子节点都无效，则可以删除。剪掉这些节点的过程，称为剪枝，目的是用来处理二叉树模型中的依赖问题。

[第814题] 给定二叉树根结点root，此外树的每个结点的值要么是0，要么是1。返回移除了所有不包含 1 的子树的原二叉树。( 节点 X 的子树为 X 本身，以及所有 X 的后代。)

  • 示例1:
    输入: [1,null,0,0,1]
    输出: [1,null,0,null,1]

    解释:
    只有红色节点满足条件“所有不包含 1 的子树”。
    右图为返回的答案。

  • 示例2:
    输入: [1,0,1,0,0,0,1]
    输出: [1,null,1,null,1]

  • 示例3:
    输入: [1,1,0,1,1,0,1,0]
    输出: [1,1,0,1,1,null,1]

说明:
给定的二叉树最多有100个节点。
每个节点的值只会为0或1。

剪什么大家应该都能理解。那关键是怎么剪？过程也很简单，在递归的过程中，如果当前结点的左右节点皆为空，且当前结点为0，我们就将当前节点剪掉即可。

1
2
3
4
5
6
7
8
9
10
#Python
class Solution:
    def pruneTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        root.left = self.pruneTree(root.left)
        root.right = self.pruneTree(root.right)
        if not root.left and not root.right and root.val == 0:
            return None
        return root

执行耗时:40 ms,击败了78.18% 的Python3用户
内存消耗:13.5 MB,击败了5.40% 的Python3用户

1
2
3
4
5
6
7
8
9
10
//Java
class Solution {
    public TreeNode pruneTree(TreeNode root) {
        if(root == null) return null;
        root.left = pruneTree(root.left);
        root.right = pruneTree(root.right);
        if(root.left == null && root.right == null && root.val == 0) return null;
        return root;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.1 MB, 在所有 Java 提交中击败了37.22% 的用户

回溯系列

1.全排列算法

什么是全排列？从 n 个不同元素中任取 m（m≤n）个元素，按照一定的顺序排列起来，叫做从 n 个不同元素中取出 m 个元素的一个排列。当 m=n 时所有的排列情况叫全排列。

[第46题] 给定一个没有重复数字的序列，返回其所有可能的全排列。

  • 示例:
    输入: [1,2,3]
    输出:
    [
    [1,2,3],
    [1,3,2],
    [2,1,3],
    [2,3,1],
    [3,1,2],
    [3,2,1]
    ]

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

比如我们选择三个数字：

  • 在枚举第一位的时候，就有三种情况
  • 在枚举第二位的时候，就只有两种情况（前面已经出现的一个数字不可以再出现）
  • 在枚举第三位的时候，就只有一种情况（前面已经出现的两个数字不可以再出现）

整个代码其实就干了这么一件事！其实就是说当枚举到最后一位的时候，这个就是我们要的排列结果，所以我们要放入到全排列结果集中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#Python
class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        self.result = []
        tmp = []
        self.dfs(nums, tmp)
        return self.result

    def dfs(self, nums, tmp):
        # 若长度相等，则添加到结果
        if len(tmp) == len(nums):
            self.result.append(tmp[:])
        else:
            for i in nums:
                if i not in tmp:
                    # 枚举第一位
                    tmp.append(i)
                    # 找出第一位固定后的排列情况
                    self.dfs(nums, tmp)
                    # 清除选择过的数字
                    tmp.pop(-1)

执行耗时:36 ms,击败了94.22% 的Python3用户
内存消耗:13.5 MB,击败了67.02% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//Java
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        dfs(nums, 0, ans);
        return ans;
    }

    public void dfs(int[] nums, int level, List<List<Integer>> ans){
        if(level == nums.length-1){
            //数组转列表
            ans.add(Arrays.stream(nums).boxed().collect(Collectors.toList()));
            return;
        }
        for(int i=level; i<nums.length; i++){
            //与当前level交换的可能
            //i = level时不动, i > level时交换
            swap(nums, i, level);
            //与下一level交换的可能
            //同理level+1可能不动，可能与大于level+1的数交换
            dfs(nums, level + 1, ans);
            //恢复
            swap(nums, i, level);
        }
    }

    public void swap(int[] nums, int i ,int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

滑动窗口系列

1.滑动窗口最大值

[第239题] 给定一个数组nums，有一个大小为k的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的k个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。

  • 示例:
    输入: nums = [1,3,-1,-3,5,3,6,7], 和k = 3
    输出: [3,3,5,5,6,7]
    解释:
    1
    2
    3
    4
    5
    6
    7
    8
      滑动窗口的位置                最大值
    ---------------               -----
    [1  3  -1] -3  5  3  6  7       3
     1 [3  -1  -3] 5  3  6  7       3
     1  3 [-1  -3  5] 3  6  7       5
     1  3  -1 [-3  5  3] 6  7       5
     1  3  -1  -3 [5  3  6] 7       6
     1  3  -1  -3  5 [3  6  7]      7

方法一：暴力求解

可以通过遍历所有的滑动窗口，找到每一个窗口的最大值，来进行暴力求解。那一共有多少个滑动窗口呢，小学题目，可以得到共有L-k+1个窗口。

1
2
3
4
5
6
7
8
9
#Python
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        result = []
        if len(nums) == 0:
            return
        for i in range(len(nums) - k + 1):
            result.append(max(nums[i: k + i]))
        return result

运行失败:
Time Limit Exceeded
运行速度不行，会超时。。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Java
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length < k) return null;
        int[] res = new int[nums.length - k + 1]; 
        int l = 0, r = k-1;
        int index = 0;
        while(r < nums.length){
            res[index++] = maxArray(nums, l, r);
            l++;
            r++;
        }
        return res;
    }

    public int maxArray(int[] nums, int l, int r){
        int maxValue = nums[l];
        for(int i = l + 1; i <= r; i++){
            if(nums[i] > maxValue) maxValue = nums[i];
        }
        return maxValue;
    }
}

Java也超时。。。。

方法二：线性题解

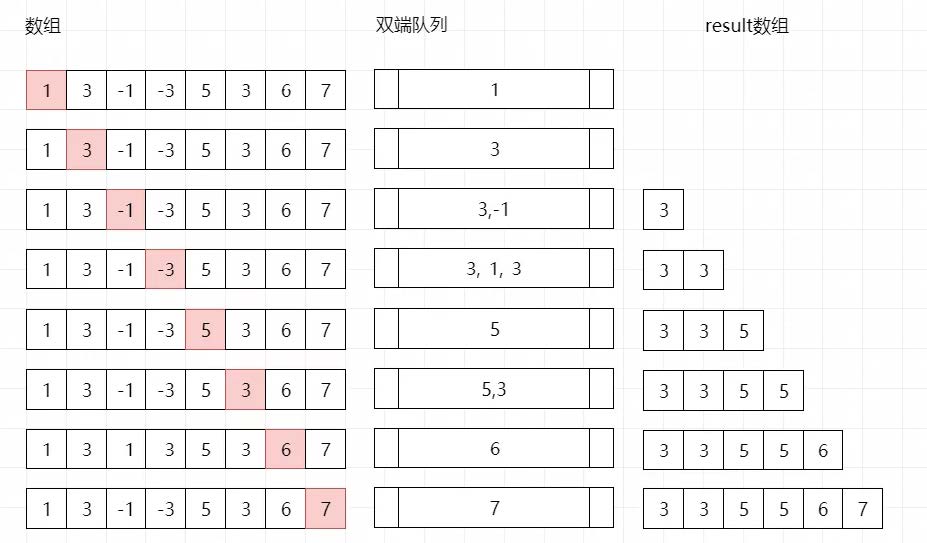
最典型的解法还是使用双端队列，只要遍历该数组，同时在双端队列的头去维护当前窗口的最大值（在遍历过程中，发现当前元素比队列中的元素大，就将原来队列中的元素祭天），在整个遍历的过程中我们再记录下每一个窗口的最大值到结果数组中。最终结果数组就是我们想要的

假设nums = [1,3,-1,-3,5,3,6,7]，和k = 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Python
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        queue = collections.deque()
        result = []
        for i in range(len(nums)):
            while i > 0 and (len(queue) > 0) and (nums[i] > queue[-1]):
                # 将比当前元素小的元素祭天
                queue.pop()
            queue.append(nums[i])
            if i >= k and nums[i - k] == queue[0]:
                # 维护队列，保证其头元素为当前窗口最大值, 而不是之前窗口
                # 即当前窗口恰好与之前窗口的最大值分离时，要舍去之前窗口的最大值
                queue.popleft()
            if i >= k-1:
                # 放入结果数组
                result.append(queue[0])

        return result

执行耗时:416 ms,击败了22.57% 的Python3用户
内存消耗:25.4 MB,击败了7.76% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//Java
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length < k) return null;
        int[] res = new int[nums.length - k + 1]; 
        //Queue窄化了LinkedList的访问,由于需要从右边弹出，这里使用LinkedList
        LinkedList<Integer> queue = new LinkedList<>();
        for(int i=0; i<nums.length; i++){
            while(i > 0 && !queue.isEmpty() && queue.peekLast() < nums[i]) queue.pollLast();
            queue.offer(nums[i]);
            if(i >= k && nums[i-k] == queue.peek()) queue.poll();
            if(i >= k-1) res[i - k + 1] = queue.peek();
        }
        return res;
    }
}

执行用时：38 ms, 在所有 Java 提交中击败了50.52% 的用户
内存消耗：52.7 MB, 在所有 Java 提交中击败了52.71% 的用户

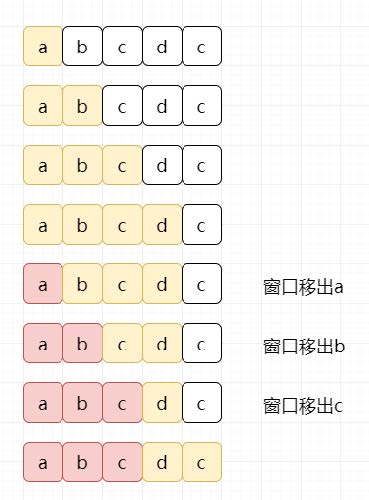
2.无重复字符的最长子串

对于大部分滑动窗口类型的题目，一般是考察字符串的匹配。比较标准的题目，会给出一个模式串B，以及一个目标串A。然后提出问题，找到A中符合对B一些限定规则的子串或者对A一些限定规则的结果，最终再将搜索出的子串完成题意中要求的组合或者其他。

而对于这一类题目，我们常用的解题思路，是去维护一个可变长度的滑动窗口。无论是使用双指针，还是使用双端队列，又或者用游标等其他奇技淫巧，目的都是一样的。

[第3题] 给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

  • 示例 1:
    输入: “abcabcbb”
    输出: 3
    解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
  • 示例 2:
    输入: “bbbbb”
    输出: 1
    解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
  • 示例 3:
    输入: “pwwkew”
    输出: 3
    解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
    请注意，你的答案必须是子串的长度，”pwke” 是一个子序列，不是子串。

方法一：双指针

假设我们的输入为“abcabcbb”，我们只需要维护一个窗口在输入字符串中进行移动。如下图：


当下一个元素在窗口没有出现过时，我们扩大窗口。


当下一个元素在窗口中出现过时，我们缩小窗口，将出现过的元素以及其左边的元素统统移出：


在整个过程中，我们记录下窗口出现过的最大值即可。而我们唯一要做的，只需要尽可能扩大窗口。

那我们代码中通过什么来维护这样的一个窗口呢？anyway~ 不管是队列，双指针，甚至通过map来
做，都可以。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#Python
class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        result = []
        left = 0
        right = 0
        maxlen = 0
        while left < len(s) and right < len(s):
            if s[right] not in result:
                result.append(s[right])
                right += 1
                maxlen = max(maxlen, right-left)
            else:
                result.remove(s[left])
                left += 1
        return maxlen

执行耗时:136 ms,击败了21.58% 的Python3用户
内存消耗:13.7 MB,击败了5.01% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//Java
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s.length() == 0) return 0;
        Set<Character> set = new HashSet<>();
        int left = 0;
        int right = 0;
        int maxLen = 0;
        while(right < s.length()){
            if(set.contains(s.charAt(right))) set.remove(s.charAt(left++));
            else set.add(s.charAt(right++));
            maxLen = Math.max(set.size(), maxLen);
        }
        return maxLen;
    }
}

执行用时：12 ms, 在所有 Java 提交中击败了23.70% 的用户
内存消耗：38.9 MB, 在所有 Java 提交中击败了23.38% 的用户

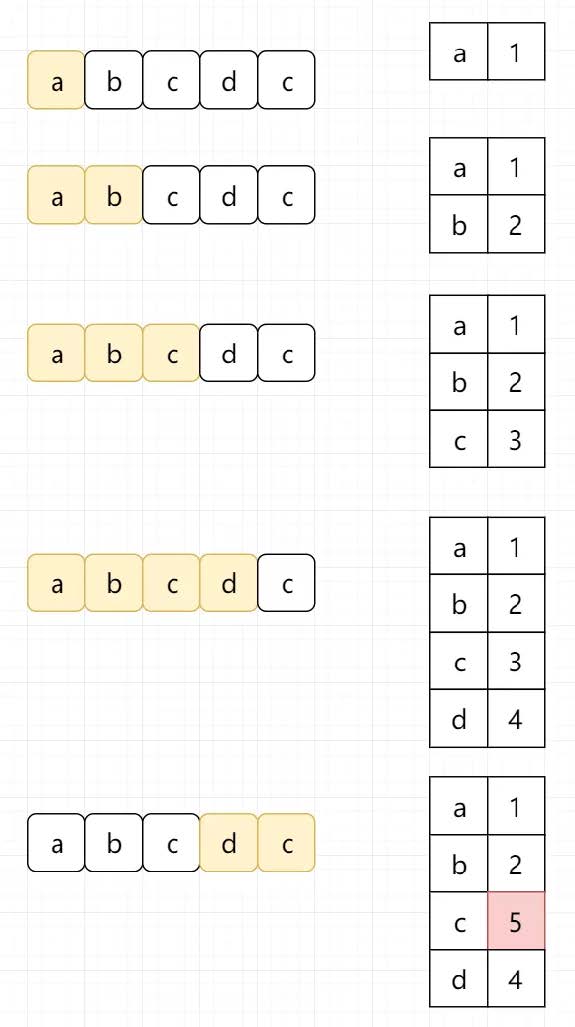
方法二：字典

通过观察，我们能看出来。如果是最坏情况的话，我们每一个字符都可能会访问两次，left一次，right一次，时间复杂度达到了O(2N)

假设我们的字符串为“abcdc”，对于abc我们都访问了2次。


那如何来进一步优化呢？其实我们可以定义字符到索引的映射，而不是简单通过一个集合来判断字符是否存在。这样的话，当我们找到重复的字符时，我们可以立即跳过该窗口，而不需要对之前的元素进行再次访问。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Python
class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        map = {}
        left = 0
        right = 0
        maxlen = 0
        while right < len(s):
            # 如果有重复字符直接跳过该窗口
            if s[right] in map:
                left = max(map[s[right]], left)
            maxlen = max(maxlen, right-left+1)
            map[s[right]] = right + 1
            right += 1
        return maxlen

执行耗时:68 ms,击败了86.27% 的Python3用户
内存消耗:13.5 MB,击败了34.59% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Java
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s.length() == 0) return 0;
        Map<Character, Integer> map = new HashMap<>();
        int left = 0;
        int right = 0;
        int maxLen = 0;
        while(right < s.length()){
            if(map.containsKey(s.charAt(right))) left = Math.max(left, map.get(s.charAt(right)));
            maxLen = Math.max(right-left+1, maxLen);
            map.put(s.charAt(right), right+1);
            right++;
        }
        return maxLen;
    }
}

执行用时：9 ms, 在所有 Java 提交中击败了40.45% 的用户
内存消耗：38.6 MB, 在所有 Java 提交中击败了61.39% 的用户

方法三：利用ASCII映射，数组代替字典

我们可以使用一个128位的数组来替代字典。（因为ASCII码表里的字符总共有128个。ASCII码的长度是一个字节，8位，理论上可以表示256个字符，但是许多时候只谈128个。具体原因可以下去自行学习~）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Python
class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        charIndex = [0]*128
        left = 0
        right = 0
        maxlen = 0
        while right < len(s):
            # 如果有重复字符直接跳过该窗口
            # ord()将字符转ASCII码
            left = max(charIndex[ord(s[right])], left)
            maxlen = max(maxlen, right-left+1)
            charIndex[ord(s[right])] = right + 1
            right += 1
        return maxlen

执行耗时:68 ms,击败了86.27% 的Python3用户
内存消耗:13.5 MB,击败了11.53% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Java
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s.length() == 0) return 0;
        int[] charIndex = new int[128];
        int left = 0;
        int right = 0;
        int maxLen = 0;
        while(right < s.length()){
            left = Math.max(left, charIndex[s.charAt(right) + 0]);
            maxLen = Math.max(right-left+1, maxLen);
            charIndex[s.charAt(right) + 0] = right + 1;
            right++;
        }
        return maxLen;
    }
}

执行用时：4 ms, 在所有 Java 提交中击败了88.31% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了40.58% 的用户

3.找到字符串中所有字母异位词

[第438题] 给定一个字符串s和一个非空字符串p，找到s中所有是p的字母异位词的子串，返回这些子串的起始索引。字符串只包含小写英文字母，并且字符串 s 和 p 的长度都不超过20100。
说明：
字母异位词指字母相同，但排列不同的字符串。
不考虑答案输出的顺序。

  • 示例 1:
    输入: s: “cbaebabacd” p: “abc”
    输出: [0, 6]
    解释:
    起始索引等于 0 的子串是 “cba”, 它是 “abc” 的字母异位词。
    起始索引等于 6 的子串是 “bac”, 它是 “abc” 的字母异位词。
  • 示例 2:
    输入: s: “abab” p: “ab”
    输出: [0, 1, 2]
    解释:
    起始索引等于 0 的子串是 “ab”, 它是 “ab” 的字母异位词。
    起始索引等于 1 的子串是 “ba”, 它是 “ab” 的字母异位词。
    起始索引等于 2 的子串是 “ab”, 它是 “ab” 的字母异位词。

我们通过双指针维护一个窗口，由于我们只需要判断字母异位词，我们可以将窗口初始化大小和目标串保持一致。

而判断字母异位词，我们需要保证窗口中的字母出现次数与目标串中的字母出现次数一致。

我们通过移动窗口，来更新窗口数组，进而和目标数组匹配，匹配成功进行记录。每一次窗口移动，左指针前移，原来左指针位置处的数值减1，表示字母移出；同时右指针前移，右指针位置处的数值加1，表示字母移入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#Python
class Solution:
    def findAnagrams(self, s: str, p: str) -> List[int]:
        # 思路:
        # 想象一个窗口在s上向右移动,窗口宽度为len(p)
        # 只要窗口内的字符串各字符数量与p中一致,则匹配成功
        # 窗口在向右移动的时候,只需要将最左端的值从字典中删除,将最右端+1的值加入字典即可.

        pmap = {}
        # 初始化目标窗口
        for i in p:
            #  get() 函数返回指定键的值, 如果键不在字典中返回默认值 None 或者设置的默认值。
            pmap[i] = pmap.get(i, 0) + 1
        plenth = len(p)

        rlist = []
        rmap = {}

        for i, v in enumerate(s):
            # 每次移动窗口，右指针值加1
            rmap[v] = rmap.get(v, 0) + 1
            # 与目标窗口匹配，返回左指针索引
            if rmap == pmap:
                rlist.append(i - plenth + 1)
            # 每次移动窗口，左指针值减1，当为0时删除
            if i - plenth + 1 >= 0:
                rmap[s[i - plenth + 1]] = rmap.get(s[i - plenth + 1]) - 1
                if rmap[s[i - plenth + 1]] == 0:
                    del rmap[s[i - plenth + 1]]

        return rlist

执行耗时:144 ms,击败了48.40% 的Python3用户
内存消耗:14.2 MB,击败了87.61% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//Java
class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        Map<Character, Integer> pmap = new HashMap<>();
        int pLength = p.length();
        for(int i=0; i<pLength; i++) pmap.put(p.charAt(i), pmap.getOrDefault(p.charAt(i), 0)+1);
        Map<Character, Integer> rList = new HashMap<>();
        List<Integer> res = new ArrayList<>();
        for(int i=0; i<s.length(); i++){
            rList.put(s.charAt(i), rList.getOrDefault(s.charAt(i), 0)+1);
            if(rList.equals(pmap)) res.add(i-pLength+1);
            if((i - pLength + 1) >= 0){
                rList.put(s.charAt(i - pLength + 1), rList.get(s.charAt(i - pLength + 1))-1);
                if (rList.get(s.charAt(i - pLength + 1)) == 0) rList.remove(s.charAt(i - pLength + 1));
            }
        }
        return res;
        
    }
}

执行用时：118 ms, 在所有 Java 提交中击败了15.26% 的用户
内存消耗：39.8 MB, 在所有 Java 提交中击败了21.13% 的用户

4.和为S的连续正数序列

[剑指57-II] 输入一个正整数target ，输出所有和为target的连续正整数序列（至少含有两个数）。序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

  • 示例 1：
    输入：target = 9
    输出：[[2,3,4],[4,5]]
  • 示例 2：
    输入：target = 15
    输出：[[1,2,3,4,5],[4,5,6],[7,8]]

假若我们输入的target为9，大脑中应该有下面这么个玩意：

然后我们通过左右指针来维护一个滑动窗口，同时计算窗口内的值是否是目标值：

如果窗口的值过小，我们就移动右边界。

如果窗口的值过大，我们就移动左边界。

剩下的就是反复上面的操作就可以了。对于任意一个正整数，总是小于它的中值与中值+1的和。

比如这里的100，就一定小于50+51，换成其他数也一样。换句话说，一旦窗口左边界超过中值，窗口内的和一定会大于target。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Python
class Solution:
    def findContinuousSequence(self, target: int) -> List[List[int]]:
        i = 1
        j = 1
        tmp = 0
        result = []
        while i <= target // 2:
            if tmp < target:
                tmp += j
                j += 1
            elif tmp > target:
                tmp -= i
                i += 1
            else:
                result.append([x for x in range(i, j)])
                tmp -= i
                i += 1
        return result

执行耗时:104 ms,击败了84.47% 的Python3用户
内存消耗:13.5 MB,击败了19.37% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Java
class Solution {
    public int[][] findContinuousSequence(int target) {
        List<int[]> list = new ArrayList<>();
        int left = 1, right = 1;
        int tmp = 0;
        while(left <= target / 2){
            if(tmp < target) tmp += right++;
            else if(tmp > target) tmp -= left++;
            else{
                int[] temp = new int[right - left];
                for (int i = 0; i < temp.length; i++) temp[i] = left + i;
                list.add(temp);
                tmp -= left++;
            }
        }
        int[][] res = new int[list.size()][];
        for (int i = 0; i < res.length; i++) {
            res[i] = list.get(i);
        }
        return res;
    }
}

执行用时：3 ms, 在所有 Java 提交中击败了79.58% 的用户
内存消耗：36.6 MB, 在所有 Java 提交中击败了47.66% 的用户

博弈论系列

本系列将为大家带来一整套的博弈论问题。因为在面试的过程中，除了常规的算法题目，我们经
常也会被问到一些趣味题型来考察思维，而这类问题中，很多都有博弈论的影子存在。这些公司里以FLAG（Facebook, LinkedIn, Amazon, Google）为典型，特别喜欢考察本类题型。同时，本系列将不一定都是算法问题，不是IT行业的小伙伴也可以进行学习，来提高分析问题的能力~

1.囚徒困境

一件严重的纵火案发生后，警察在现场抓到两个犯罪嫌疑人。事实上，正是他们一起放火烧了这座仓库。但是，警方没有掌握足够的证据，只得把他们分开囚禁起来，要求他们坦白交代。

在分开囚禁后，警察对其分别告知：
如果你坦白，而对方不坦白，则将你释放，判对方8年。
如果你不坦白，而对方坦白，则将对方释放，而判你8年。
如果你两都坦白了，则判你两各自4年。
那么两个囚犯应该如何做，是互相背叛还是一起合作？

题目分析 从表面上看，其实囚犯最应该的就是一起合作，都不坦白，这样因为证据不足，会将两人都进行释放。
但是！因为事实确实是两人放的火，所以他们不得不进行思考，另一人采取了什么样的行为？

犯人甲当然不傻，他根本无法相信同伙不会向警方提供任何信息！因为如果同伙一旦坦白，而自己这边如果什么都没说的话，就可以潇洒而去。但他同时也意识到，他的同伙也不傻，也会同样来这样设想他。

所以犯人甲的结论是，唯一理性的选择就是背叛同伙，把一切都告诉警方！这样的话，如果他的同伙笨得只会保持沉默，那么他就会是那个离开的人。而如果他的同伙也根据这个逻辑向警方交代了，那么也没有关系，起码他不必服最重的刑！

这场博弈的过程，显然不是顾及团体利益的最优解决方案。以全体利益而言，如果两个参与者都合作保持沉默，两人都可以无罪释放，总体利益更高！但根据假设（人性），二人均为理性的个人，且只追求自己的个人利益。均衡状况会是两个囚徒都选择背叛，这就是“困境”所在！

事实上，这种两人都选择坦白的策略以及因此被判4年的结局被称作“纳什均衡”（也叫非合作均衡），换言之，在此情况下，无一参与者可以“独自行动”（即单方面改变决定）而增加收获。

我们看一下官方释意是多么难懂“所谓纳什均衡，指的是参与人的一种策略组合，在该策略组合上，任何参与人单独改变策略都不会得到好处。”简单点讲，如果在一个策略组合上，当所有其他人都不改变策略时，没有人会改变自己的策略，则该策略组合就是一个纳什均衡。

2.辛普森悖论

羊羊医院里统计了两种胆结石治疗方案的治愈率。在统计过程中，医生将病人分为大胆结石和小胆结石两组。统计结果如下：

  • 对于小胆结石而言，手术A的治愈率（93%）高于手术B（87%）
  • 对于大胆结石而言，手术A的治愈率（73%）高于手术B（69%）

羊羊医院的医生得出结论：

无论是对于大小胆结石，手术A的治愈率都胜过手术B。

但是真的是这样吗？当然不是，我们根据样本统计出大小胆结石总计的治愈率，发现手术B(治愈率83%)其实是要高于手术A(治愈率78%)。

为什么会出现这样的结果？这就是著名的辛普森悖论。

题目分析 得到了结论，我们来思考背后的东西。在我们的直觉里有这样一个逻辑：如果一个事物的各部分都分别大于另一个事物的各部分，那么这个事物大于另一个事物。比如：我们的直觉告诉我们如果手术A在两组病人中都更好，那么在所有病人中也应该更好。
我们可以将其公式化（该公式错误），假设：

A=A1+A2+….+An
B=B1+B2+….+Bn
如果对i=1,2…,n都有Ai>Bi，则A>B

乍一看，我们觉得该公式没有问题，所以这个公式也就代表了我们大部分人的思维工作。其实在这个公式中，隐藏掉了一个很重要的条件：A1、A2、An 以及 B1、B2、Bn 并不能简单的通过“加”来得到 A或者B。这就是可加性的前提。在大脑的思维过程中，因为我们很难直接看到这个前提，进而就导致了我们错误的思考！

下面我们举一些在生活中常见的辛普森悖论例子：

  • 打麻将的时候，把把都赢小钱，造成赢钱的假象，其实不如别人赢一把大的。
  • 在苹果和安卓的竞争中，你听见身边的人都在逃离苹果，奔向安卓。但是其实苹果的流入率还是要高于安卓。（有数据证明，很经典的案例）
  • 你男票，这里比别人差，那里比别人差，但是其实他真的比别的男生差吗？（这个纯属本人胡扯了..）

3.红眼睛和蓝眼睛

一个岛上有100个人，其中有5个红眼睛，95个蓝眼睛。这个岛有三个奇怪的宗教规则。

1.他们不能照镜子，不能看自己眼睛的颜色。
2.他们不能告诉别人对方的眼睛是什么颜色。
3.一旦有人知道了自己是红眼睛，他就必须在当天夜里自杀。

某天，有个旅行者到了这个岛上。由于不知道这里的规矩，所以他在和全岛人一起狂欢的时候，不留神就说了一句话：【你们这里有红眼睛的人。】

问题：假设这个岛上的人每天都可以看到其他所有人，每个人都可以做出缜密的逻辑推理，请问岛上会发生什么？

题目分析 题目乍看之下，没有任何逻辑可言！以目测条件，基本无法完成任何正常的推理。但是在仔细推敲之后，我们可以将问题简化，从假设只有1个红眼睛开始分析。

我们假设岛上只有1个红眼睛的人，还有99个都是蓝眼睛。因为这个旅行者说了“这里有红眼睛的人”，那么在第一天的时候，这个红眼睛会发现其他的人都是蓝眼睛（与此同时，其他人因为看到了这个红眼睛的人，所以都确认了自己的安全）那么这天晚上，这个红眼睛的人一定会自杀！

继续分析，假设这个岛上有2个红眼睛，那么当旅行者说“这里有红眼睛的人”之后的第一天，这两个红眼睛分别发现还有别的红眼睛存在，所以他们当天晚上认为自己是安全的。但是到了第二天，红眼睛惊讶的发现，另一个红眼睛的人竟然没有自杀（说明岛上有不止一个红眼睛），并且当天他们也没有发现有别的红眼睛存在（说明另一个红眼睛就是自己）WTF，那肯定另一个红眼睛就是自己了，所以在第二天夜里，两个红眼睛的人会同时自杀！

继续分析，假如岛上红眼睛有3个。那么在第一天，红眼睛发现了岛上还有另外两个红眼睛，红眼睛呵呵一笑，“反正不是我”。到了第二天，红眼睛仍然看到了另外两个红眼睛，红眼睛心想，”这下你两该完蛋了吧”，毕竟你两都知道了自己是红眼睛，晚上回去统统自杀吧！（根据上面的推论得出）但是惊奇的是，到了第三天，红眼睛发现另外两个红眼睛竟然都没有自杀。（说明岛上红眼睛的人不止两个）并且当天红眼睛也没发现新的红眼睛（说明还有一个红眼睛就是自己）所以在第三天的夜里，三个红眼睛会同时自杀。

根据上面的推论，假设有N个红眼睛，那么到了第N天，这N个红眼睛就会自杀。所以最终这个岛上红眼睛的人会统统自杀！这就是答案，生活就是这么朴实无华，且枯燥。

旅客的挽回
上面的分析大家应该都看懂了。但若是在旅客说完这句话后，其并没有离开这个岛。同时他也看到了周围人眼里的惊慌和失措，这个时候，旅客为自己的行为感到了懊恼和悔恨！旅客决定对自己的话进行挽回，旅客又该怎么做呢？

这里我提供一种思路，旅客可以在第N次集会上杀掉N个红眼睛，让这N个红眼睛 “GO TO SLEEP”，就可以中断事件的推理。事实上，基于人道主义，旅客并不需要手动杀人，她只需要在第N天的时候告诉这N个人，你们是红眼睛，那么这天晚上，这N个人就会自杀。”All RETURN”，一切将回归秩序~

4.海盗分金币

在大海上，有5个海盗抢得100枚金币，他们决定每一个人按顺序依次提出自己的分配方案，如果提出的方案没有获得半数或半数以上的人的同意，则这个提出方案的人就被扔到海里喂鲨鱼。那么第一个提出方案的人要怎么做，才能使自己的利益最大化？

海盗们有如下特点：
1.足智多谋，总是采取最优策略。
2.贪生怕死，尽量保全自己性命。
3.贪得无厌，希望自己得到越多宝石越好
4.心狠手辣，在自己利益最大的情况下希望越多人死越好。
5.疑心多虑，不信任彼此，尽量确保自身利益不寄希望与别人给自己更大利益。

题目分析 首先我们很容易会觉得，抽签到第一个提方案的海盗会很吃亏！因为只要死的人够多，那么平均每个人获取的金币就最多，而第一个提方案的人是最容易死的。但是事实是，在满足海盗特点的基础上，第一个提方案的海盗是最赚的，我们一起来分析一下。

假如我们设想只有两个海盗。那么不管第一个说什么，只要第二个人不同意，第二个人就可以得到全部的金币！所以第一个海盗必死无疑，这个大家都能理解。（当然，这样的前提是一号提出方案后不可以马上自己同意，不然如果自己提出给自己全部金币的方案，然后自己支持，这样就是二号必死无疑）

假如现在我们加入第三个海盗，这时候原来的一号成为了二号，二号成为了三号。这时候现在的二号心里会清楚，如果他投死了一号，那么自己必死无疑！所以根据贪生怕死的原则，二号肯定会让一号存活。而此时一号心理也清楚，无论自己提出什么样的方案，二号都会让自己存活，而这时只要加上自己的一票，就有半数通过，所以一号提出方案：把金币都给我。

现在又继续加入了新的海盗！原来的1,2,3号，成为了现在的2,3,4号。这时候新的一号海盗洞悉了奥秘，知道了如果自己死了，二号就可以获取全部的金币，所以提出给三号和四号一人一个金币，一起投死2号。而与此同时，现在的3号和4号获取的要比三个人时多（三个人时自己获取不了任何金币），所以他们会同意这个方案！

现在加入我们的大Boss，最后一个海盗。根据分析，大Boss海盗1号推知出2号的方案后就可以提出(97,0,1,2,0)或者(97,0,1,0,2)的方案。这样的分配方案对现在的3号海盗相比现在的2号的分配方案还多了一枚金币，就会投赞成票，4号或者5号因为得到了2枚金币，相比2号的一枚多，也会支持1号，加上1号自己的赞成票，方案就会通过，即1号提出(97,0,1,2,0)或(97,0,1,0,2)的分配方案，大Boss成功获得了97枚金币。

思考 最终，大Boss一号海盗得到97枚金币，投死了老二和老五，这竟然是我们分析出的最佳方案！这个答案明显是反直觉的，如果你是老大，你敢这样分金币，必死无疑。可是，推理过程却非常严谨，无懈可击，那么问题出在哪里呢？

其实，在”海盗分赃”模型中，任何”分配者”想让自己的方案获得通过的关键是，事先考虑清楚”对手”的分配方案是什么，并用最小的代价获取最大收益，拉拢”对手”分配方案中最不得意的人们。1号看起来最有可能喂鲨鱼，但他牢牢地把握住先发优势，结果不但消除了死亡威胁，还收益最大。而5号，看起来最安全，没有死亡的威胁，甚至还能坐收渔人之利，却因不得不看别人脸色行事而只能分得一小杯羹。

不过，模型任意改变一个假设条件，最终结果都不一样。而现实世界远比模型复杂。因为假定所有人都理性，本身就是不理性的。回到“海盗分金”的模型中，只要3号、4号或5号中有一个人偏离了绝对聪明的假设，海盗1号无论怎么分都可能会被扔到海里去了。所以，1号首先要考虑的就是他的海盗兄弟们的聪明和理性究竟靠得住靠不住，否则先分者必定倒霉。

如果某人和一号本身不对眼，就想丢他喂鲨鱼。果真如此，1号自以为得意的方案岂不成了自掘坟墓。再就是俗话所说的“人心隔肚皮”。由于信息不对称，谎言和虚假承诺就大有用武之地，而阴谋也会像杂草般疯长，并借机获益。如果2号对3、4、5号大放烟幕弹，宣称对于1号所提出任何分配方案，他一定会再多加上一个金币给他们。这样，结果又当如何？

通常，现实中人人都有自认的公平标准，因而时常会嘟嚷：“谁动了我的奶酪？”可以料想，一旦1号所提方案和其所想的不符，就会有人大闹。当大家都闹起来的时候，1号能拿着97枚金币毫发无损、镇定自若地走出去吗？最大的可能就是，海盗们会要求修改规则，然后重新分配。当然，大家也可以讲清楚下次再得100枚金币时，先由2号海盗来分…然后是3号……颇有点像美国总统选举，轮流主政。说白了，其实是民主形式下的分赃制。

最可怕的是其他四人形成一个反1号的大联盟并制定出新规则：四人平分金币，将1号扔进大海。这就颇有点阿Q式的革命理想：高举平均主义的旗帜，将富人扔进死亡深渊。

5.智猪博弈

假设猪圈里有一头大猪、一头小猪。猪圈的一头有猪食槽，另一头安装着控制猪食供应的按钮，按一下按钮会有10个单位的猪食进槽，,但是按按钮以后跑到食槽所需要付出的劳动量，加起来要消耗相当于2个单位的猪食。并且因为按钮和食槽分置笼子的两端，等到按按钮的猪付出劳动跑到食槽的时候，坐享其成的另一头猪早已吃了不少。如果大猪先到（小猪按），大猪吃掉9个单位，小猪只能吃到1个单位；如果同时到达（也就是一起按），大猪吃掉7个单位，小猪吃到3个单位；如果小猪先到（大猪按），小猪可以吃到4个单位，而大猪吃到6个单位。那么，在两头猪都足够聪明的前提下，最终的结果是什么？

首先小猪如果去按按钮，然后再回来的话，只能吃到一份猪食，直接就嗝屁了，这种可能性肯定是不行的。自然，这时大猪也就只有去按按钮这一个选项了。所以最终的结果会是：小猪选择等待，大猪去按按钮。

  • 如果小猪和大猪同时行动的话，则它们同时到达食槽，分别得到1个单位和5个单位的纯收益（付出4个单位的成本）

  • 如果大猪行动，小猪等待，小猪可得到4个单位的纯收益，大猪得到的6个单位，付出2个单位的成本，实得4个单位；

  • 如果大猪等待，小猪行动，小猪只能吃到1个单位，则小猪的收入将不抵成本，纯收益为-1。

  • 如果大猪等待，小猪也等待，那么小猪的收益为零，成本也为零，总之，小猪等待还是要优于行动。

这道题目是一个很经典的“劣势策略”下的可预测问题，其在各高校经济学课程中也被放在一个举足轻重的地位上。原因无他，正是大猪做出这样一个“决策”，目的不是出于对小猪的爱，而是基于“自利”的原则。

6.生男生女问题

题目：国家为了调控男女比例，制定了一个政策：新婚夫妇都必须生娃（接地气），如果生出的是男娃就不能再生了，如果生出的是女娃就必须继续生下去，直到生出第一个男娃为止（出题人牛P）。
问题是：若干年后，该国的男女比例会发生怎样的变化？

其实这个问题答案是比较反直觉的：没有变化。原因是因为：生男生女的概率永远都是百分之50。

或者我们也可以换一种思路：我们不妨假设把一大批新婚夫妇关在一个超大的屋子里，逼着他们进行一轮一轮的生孩子游戏。第一轮里，有一半的夫妇生了男娃，退出了游戏；另一半夫妇得到的是女娃，进入第二轮。在第二轮里面，又有一半由于生出男娃而退出，自然，另一半生出女娃的夫妇进入第三轮……注意到，在每一轮里，新生男娃和新生女娃都是一样多的，因此把所有轮数合在一起看，男娃的总数和女娃的总数也一定是相同的。

7.硬币问题

题目：A和B两人为了竞价一个拍卖品，决定用抛掷硬币的办法来判断谁有资格。为了让游戏过程更加刺激，A提出了这样一个方案：连续抛掷硬币，直到最近三次硬币抛掷结果是“正反反”或者“反反正”。如果是前者，那么A获胜；如果是后者，那么B获胜
问题是：B应该接受A的提议吗？换句话说，这个游戏是公平的吗？

事实，该游戏并不公平。虽然“正反反”和“反反正”在频率上出现的一样，但是其之间却有一个竞争关系：一旦抛硬币产生其中一种序列，游戏即结束。所以不论何时，只要抛出一个正面，也就意味着B必输无疑。换句话说，在整个游戏的前两次抛掷中，只要出现“正正”，“正反”，“反正”其中任一，A则一定会取得胜利。A和B的概率比达到3:1，优势不言而喻。

8.画圈圈的问题

面试题：小浩出去面试时，面试官拿出一张纸，在纸上从左到右画了一百个小圆圈（手速快，没办法）接下来，面试官要求两人轮流涂掉其中一个或者两个相邻的小圆圈。
规定：谁涂掉最后一个小圆圈谁就赢了（换句话说，谁没有涂的了谁就输了）。问题是：小浩应该选取先涂还是后涂？如何才能有必胜策略？

作为聪明机智的小浩（没见过这么夸自己的），最后当然是小浩获胜。获胜的方法：小浩强烈要求先手进行游戏，并且在游戏开始时，先把正中间的两个小圆圈涂黑，于是左右两边各剩下了49个圆圈。像是下面这样：


然后小浩开始模仿（逼死）面试官，面试官在左边涂掉哪些圆圈，小浩就对称地在右边涂掉哪些圆圈；面试官在右边涂掉哪些圆圈， 小浩就对称地在左边涂掉哪些圆圈。因此，只要面试官有走的，小浩就一定有走的，最终保证能获胜。

在博弈论中，这类游戏就叫做“无偏博弈”（impartial game）。在无偏博弈中，如果对于某个棋局状态，谁遇到了它谁就有办法必胜，我们就把它叫做“必胜态”；如果对于某个棋局状态，谁遇到了它对手就会有办法必胜，我们就把它叫做“必败态”。

9.巧克力问题

面试题：小浩出去面试时，面试官掏出一块10×10个小块的巧克力。首先，面试官把巧克力掰成两大块，并且吃掉其中一块，把另一块交给小浩。小浩再把剩下的巧克力掰成两大块，吃掉其中一块，把另一块交回给面试官。两个人就这样无聊且枯燥的掰呀掰。。。
规定：谁没办法往下继续掰，谁就输了。如果面试官先开始掰的话，面试官和小浩谁有必胜策略？（面试官输了，小浩将赢得面试）

作为聪明机智的小浩（没见过这么夸自己的），最后当然是小浩获胜。获胜的方法：只要小浩一直保持巧克力是正方形就可以了。不管面试官咋掰，最后都会掰成一个长宽不相等的正方形。直到最后一次将其变成一个1×1的巧克力，此时面试官就输掉了面试。哦不，是小浩赢得了面试。

[超级改编版] 如果巧克力换成边长为10的等边三角形，长这样：

每次只能沿着线条掰下一个小等边三角形吃掉，假若还是由面试官开局，请问，谁必胜？

等边三角形是小浩赢。

1.面试官先手沿着任意一条线掰开。
2.剩下的等腰梯形中，小浩从面试官掰开处将等腰梯形掰成等边三角形和平行四边形，将平行四边形还给面试官。
3.面试官在平行四边形的两个角中任意掰出个等边三角形。
4.小浩掰另一个角大小跟面试官一致，此时剩下的巧克力有三种可能的形态：

  • 平行四边形缺了两个小角：此形状给面试官 他已经没有办法掰出一个等边三角形。面试官输了。
  • 依然是平行四边形：陷入此步循环，直到掰没了：最后的平行四边形可以由两个等边三角形组合而成，小浩后掰，小浩赢了。

10.大鱼和小鱼的问题

大鱼小鱼的问题：假设有10条鱼，它们从小到大依次编号为1, 2, …, 10。我们规定，吃鱼必须要严格按顺序执行。也就是说，大鱼只能吃比自己小一级的鱼，不能越级吃更小的鱼；并且只有等到第k条鱼吃了第k-1条鱼后，第k+1条鱼才能吃第k条鱼。
同时：第1条鱼则啥都不能吃，只有被吃的份儿。我们假设，如果有小鱼吃的话，大鱼肯定不会放过；但是，保全性命的优先级显然更高，在吃小鱼之前，大鱼得先保证自己不会被吃掉才行。假设每条鱼都是无限聪明的（并且它们也都知道这一点，并且它们也都知道它们知道这一点……），那么第1条鱼能存活下来吗？

我们是有十条鱼，分析起来是比较麻烦的。所以我们从最简单的两条鱼开始分析：


两条鱼的情况下，第二条鱼就是无敌的存在，他不用担心自己被吃掉！如果是三条鱼：

3条鱼的情况下，第2条鱼不能吃第1条鱼，否则将化为只有2条鱼的情形，它将会被第3条鱼吃掉。如果是四条鱼，就有意思了：

此时第2条鱼可以大胆地吃掉第1条鱼，因为根据前面的结论，它知道第3条鱼是不敢吃它的。问题来了，五条鱼会如何：

5条鱼的情况下，第2条鱼是不敢吃第1条鱼的，因为如果它吃了第一条鱼。问题转化为4条鱼的场景，原3号鱼就可以大胆吃掉原2号鱼，因为它知道4号鱼是不敢吃它的，否则5号鱼就会吃掉4号鱼（绕不绕）。

我们发现一个有趣的结论，只要鱼有奇数个，那么第一条鱼将总是可以活下来。如果鱼是偶数个，那么第二条鱼将总是可以吃掉第一条鱼，将状态转化到奇数条鱼的场景。

所以该题的答案是：不能，在十条鱼的场景下，第一条鱼必死无疑。

排序系列

1.按奇偶排序数组

插入排序：就是炸金花的时候，你接一个同花顺的过程。（标准定义：在要排序的一组数中，假定前n-1个数已经排好序，现在将第n个数插到前面的有序数列中，使得这n个数也是排好顺序的）

[第905题] 给定一个非负整数数组A，返回一个数组，在该数组中， A的所有偶数元素之后跟着所有奇数元素。你可以返回满足此条件的任何数组作为答案。

  • 示例：
    输入：[3,1,2,4]
    输出：[2,4,3,1]
    输出 [4,2,3,1]，[2,4,1,3] 和 [4,2,1,3] 也会被接受。

这道题，按照插入排序的思想，很容易可以想到题解。我们只需要遍历数组，当我们遇到偶数时，将其插入到数组前最近的一个为奇数的位置，与该位置的奇数元素交换。为了达成该目的，我们引入一个指针 j，来维持这样一个奇数的位置。

假设我们的数组为：[3,1,2,4]

1
2
3
4
5
6
7
8
9
#Python
class Solution:
    def sortArrayByParity(self, A: List[int]) -> List[int]:
        j = 0
        for i in range(len(A)):
            if A[i] % 2 == 0:
                A[j], A[i] = A[i], A[j]
                j += 1
        return A

执行耗时:100 ms,击败了61.73% 的Python3用户
内存消耗:13.9 MB,击败了50.05% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//Java
class Solution {
    public int[] sortArrayByParity(int[] A) {
        int j = 0;
        for(int i = 0; i < A.length; i++){
            if(A[i] % 2 == 0) swap(A, i, j++);
        }
        return A;
    }

    public void swap(int[] A, int i, int j){
        int tmp = A[i];
        A[i] = A[j];
        A[j] = tmp;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：39.6 MB, 在所有 Java 提交中击败了5.02% 的用户

位运算系列

1.使用位运算求和

该题很容易出现在各大厂的面试中，属于必须掌握的题型。

[剑指offer 64] 求 1 2 … n ，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

  • 示例 1：
    输入: n = 3 输出: 6
  • 示例 2：
    输入: n = 9 输出: 45
  • 限制：
    1 <= n <= 10000

题目上手，因为不能使用公式直接计算（公式中包含乘除法），所以考虑使用递归进行求解，但是递归中一般又需要使用if来指定返回条件（这里不允许使用if），所以没办法使用普通的递归思路。

首先我们了解一下 && 的特性，比如有 A&&B
如果A为true，返回B的布尔值（继续往下执行）
如果A为false，直接返回false（相当于短路）

利用这一特性，我们将递归的返回条件取非然后作为 && 的第一个条件，递归主体转换为第二个条件语句。

1
2
3
4
#Python
class Solution:
	def sumNums(self, n: int) -> int:
		return n and (n + self.sumNums(n-1))

执行用时：48 ms, 在所有 Python 提交中击败了10.79% 的用户
内存消耗：20.1 MB, 在所有 Python 提交中击败了37.95% 的用户

1
2
3
4
5
6
7
//Java
class Solution {
    public int sumNums(int n) {
        boolean b = n > 0 && (n += sumNums(n - 1)) > 0;
        return n;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了58.91% 的用户
内存消耗：35.8 MB, 在所有 Java 提交中击败了28.19% 的用户

2.2的幂

[第231题] 给定一个整数，编写一个函数来判断它是否是2的幂次方。

  • 示例 1:
    输入: 1
    输出: true
    解释: $2^0 $= 1
  • 示例 2:
    输入: 16
    输出: true
    解释: $2^4$ = 16
  • 示例 3:
    输入: 218
    输出: false

先观察一些是2的幂的二进制数：


然后我们再观察下面这样的一组数，对应着上面的数减去1：


我们对两组数求“&”运算：


可以看到，对于N为2的幂的数，都有 N&(N-1)=0 ，所以这就是我们的判断条件。（这个技巧可以记忆下来，在一些别的位运算的题目中也是会用到的）

1
2
3
4
#Python
class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        return n > 0 and n & (n-1) == 0

执行耗时:52ms,击败了17.68% 的Python3用户
内存消耗:13.3 MB,击败了77.73% 的Python3用户

1
2
3
4
5
6
7
//Java
class Solution {
    public boolean isPowerOfTwo(int n) {
        //a % b 若b为2的整数次幂，则该式等价于a与b-1的位与
        return n > 0 && ((n & (n-1)) == 0);
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.6 MB, 在所有 Java 提交中击败了28.30% 的用户

3.返回一个数二进制中1的个数

[第191题] 编写一个函数，输入是一个无符号整数，返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

  • 示例 1：
    输入：00000000000000000000000000001011
    输出：3
    解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。
  • 示例 2：
    输入：00000000000000000000000010000000
    输出：1
    解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 ‘1’。
  • 示例 3：
    输入：11111111111111111111111111111101
    输出：31
    解释：输入的二进制串 11111111111111111111111111111101 中，共有31位为 ‘1’。

提示：
请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的示例3中，输入表示有符号整数-3。

方法一

这道题仍然是通过位运算来进行求解的非常典型的题目。掩码是指使用一串二进制代码对目标字段进行位与运算，屏蔽当前的输入位。

我们直接把目标数转化成二进制数，然后遍历每一位看看是不是1，如果是1就记录下来。

我们可以构造一个掩码来进行，其实就是弄个1出来，1的二进制是这样：


我们只需要让这个掩码每次向左移动一位，然后与目标值求“&”，就可以判断目标值的当前位是不是1。比如目标值为21，21的二进制是这样：


然后每次移动掩码，来和当前位进行计算：

1
2
3
4
5
6
7
8
9
10
#Python
class Solution:
    def hammingWeight(self, n: int) -> int:
        mask = 1
        result = 0
        for i in range(32):
            if (n & mask) != 0:
                result += 1
            mask <<= 1
        return result

执行耗时:40 ms,击败了75.02% 的Python3用户
内存消耗:13.4 MB,击败了26.44% 的Python3用户

注意：这里判断 n&mask 的时候，千万不要错写成 (n&mask) == 1，因为这里你对比的是十进制数。

1
2
3
4
5
6
7
8
9
10
11
12
//Java
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count = 0;
        for(int i = 0; i < 32; i++) {
            count += n & 1;    
            n >>>= 1; //无符号右移
        }
        return count;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.7 MB, 在所有 Java 提交中击败了5.02% 的用户

方法二

位运算小技巧: 对于任意一个数，将 n 和 n-1 进行 & 运算，我们都可以把 n 中最低位的 1 变成 0

我们拿 11 举个例子：（注意最后一位1变成0的过程）

1
2
3
4
5
6
7
8
#Python
class Solution:
    def hammingWeight(self, n: int) -> int:
        result = 0
        while n != 0:
            n = n & (n-1)
            result += 1
        return result

执行耗时:40 ms,击败了75.02% 的Python3用户
内存消耗:13.6 MB,击败了5.40% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
//Java
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count = 0;
        while(n != 0) {
            n &= (n-1);    
            count++;
        }
        return count;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了95.92% 的用户
内存消耗：35.1 MB, 在所有 Java 提交中击败了94.71% 的用户

方法三：利用Python内置方法

1
2
3
4
#Python
class Solution:
    def hammingWeight(self, n: int) -> int:
        return bin(n).count('1')

执行耗时:40 ms,击败了75.02% 的Python3用户
内存消耗:13.6 MB,击败了5.40% 的Python3用户

4.只出现一次的数字

[第136题] 给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
说明：
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

  • 示例 1:
    输入: [2,2,1]
    输出: 1
  • 示例 2:
    输入: [4,1,2,1,2]
    输出: 4

对于任意两个数a和b，我们对其使用 “异或”操作，应该有以下性质：

任意一个数和0异或仍然为自己：a⊕0 = a

任意一个数和自己异或是0：a⊕a=0

异或操作满足交换律和结合律：a⊕b⊕a=(a⊕a)⊕b=0⊕b=b

因为其余元素均出现两次，所以根据异或操作的交换律和结合律对数组进行迭代，最终留下的就是只出现一次的数字

1
2
3
4
5
6
7
#Python
class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        res = 0
        for i in range(len(nums)):
            res ^= nums[i]
        return res

执行耗时:52 ms,击败了46.94% 的Python3用户
内存消耗:15.1 MB,击败了34.55% 的Python3用户

1
2
3
4
5
6
7
8
//Java
class Solution {
    public int singleNumber(int[] nums) {
        int res = 0;
        for(int num: nums) res ^= num;
        return res;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.1 MB, 在所有 Java 提交中击败了99.75% 的用户

5.只出现一次的数字Ⅱ

[第137题] 给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。说明：你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

  • 示例 1:
    输入: [2,2,3,2]
    输出: 3
  • 示例 2:
    输入: [0,1,0,1,0,1,99]
    输出: 99

方法一：HashMap求解

很简单就能想到，说白了就是统计每个元素出现的次数，最终再返回次数为1的元素。但是使用了额外空间。

1
2
3
4
5
6
7
8
9
10
11
12
#Python
class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        map = {}
        for i in nums:
            if i in map:
                map[i] += 1
            else:
                map[i] = 1
        for i in map:
            if map[i] == 1:
                return i

执行耗时:40 ms,击败了89.49% 的Python3用户
内存消耗:14.8 MB,击败了19.68% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
//Java
class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int num: nums) map.put(num, map.getOrDefault(num, 0)+1);
        for(int key: map.keySet()){
            if(map.get(key) == 1) return key;
        }
        return -1;
    }
}

执行用时：7 ms, 在所有 Java 提交中击败了9.09% 的用户
内存消耗：38.2 MB, 在所有 Java 提交中击败了55.72% 的用户

方法二：数学方式

原理：[A,A,A,B,B,B,C,C,C] 和 [A,A,A,B,B,B,C]，差了两个C。即：3×(a b c)−(a a a b b b c)=2c

也就是说，如果把原数组去重、再乘以3得到的值，刚好就是要找的元素的2倍。

1
2
3
4
#Python
class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        return int((sum(set(nums)) * 3 - sum(nums)) / 2)

执行耗时:36 ms,击败了96.69% 的Python3用户
内存消耗:14.7 MB,击败了26.89% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//Java
class Solution {
    public int singleNumber(int[] nums) {
        Set<Integer> key = new HashSet<>();
        long sum1 = 0;
        for(int num: nums) {
            key.add(num);
            sum1 += num;
        }
        long sum2 = 0;
        for(int num: key) sum2 += num;
        return (int)((3 * sum2 - sum1) / 2);
    }
}

执行用时：4 ms, 在所有 Java 提交中击败了37.02% 的用户
内存消耗：38.1 MB, 在所有 Java 提交中击败了85.08% 的用户

方法三：位运算

对于“每个其余元素，均出现了二次”之所以可以使用“异或”进行求解，原因是因为“异或”操作可以让两数相同归0。那对于其余元素出现三次的，是不是只要可以让其三者相同归0，就能达到我们的目的呢？

因为各语言中都没有这样一个现成的方法可以使用，所以我们需要构造一个。（想象一下，位运算也是造出来的对不对？）

异或运算是不是可以理解为，其实就是二进制的加法，然后砍掉进位呢？砍掉进位的过程，是不是又可以理解为对 2 进行取模，也就是取余。到了这里，问题已经非常非常明确了。那我们要完成一个 a ? a ? a = 0 的运算，是不是其实就是让其二进制的每一位数都相加，最后再对3进行一个取模的过程呢？（一样，如果要定义一个 a ? a ? a ? a = 0 的运算，那就最后对4进行取模就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#Python
class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        # python中int为变长的，所以定义32位的列表
        count = [0] * 32
        res = 0
        for i in range(32):
            # 每一位都对对应位上的所有数做和
            for j in nums:
                # 判断该数是否为负数
                if j < 0:
                    j = j & 0xffffffff
                # 记录该位1的个数
                if (j >> i) & 1 == 1:
                    count[i] += 1
            # 最终将抵消后剩余的1放到对应的位数上
            if count[i] % 3 == 1:
                res |= 1 << i
        # 判断结果正负
        return res if res <= 0x7FFFFFFF else ~(res ^ 0xFFFFFFFF)

执行耗时:124 ms,击败了13.36% 的Python3用户
内存消耗:14.7 MB,击败了28.80% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//Java
class Solution {
    public int singleNumber(int[] nums) {
        int[] count = new int[32];
        int res = 0;
        for(int i = 0; i < 32; i++){
            for(int num: nums){
                if(((num >>> i) & 1) == 1) count[i] += 1;
            }
            if(count[i] % 3 == 1) res += (1 << i);
        }
        return res;
    }
}

执行用时：4 ms, 在所有 Java 提交中击败了37.02% 的用户
内存消耗：38.5 MB, 在所有 Java 提交中击败了9.53% 的用户

在上面的代码中，我们记录每一位数出现的次数。但是缺点是，我们记录了32位。那如果我们可以同时对所有位进行计数，是不是就可以简化过程。因为我们的目的是把每一位与3取模进行运算，是不是就可以理解为其实是一个三进制。所以我们就只有3个状态，00 - 01 - 10，所以我们采用 a 和 b 来记录状态。其中的状态转移过程如下：

这里 a‘ 和 b’ 的意思代表着 a 和 b 下一次的状态。next 代表着下一个 bit 位对应的值。

写出关系式：

1
2
b = (b ^ next) & ~a;
a = (a ^ next) & ~b; #注意这里的b已经变了，是上式求得的b
1
2
3
4
5
6
7
8
#Python
class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        a, b = 0, 0
        for next in nums:
            b = (b ^ next) & ~a
            a = (a ^ next) & ~b
        return b

执行耗时:36 ms,击败了96.69% 的Python3用户
内存消耗:14.6 MB,击败了38.94% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
//Java
class Solution {
    public int singleNumber(int[] nums) {
        int a = 0, b = 0;
        for(int next: nums){
            b = (b ^ next) & ~a;
            a = (a ^ next) & ~b;
        }
        return b;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.2 MB, 在所有 Java 提交中击败了58.04% 的用户

6.缺失数字

[第268题] 给定一个包含[0, n]中n个数的数组nums ，找出[0, n]这个范围内没有出现在数组中的那个数。进阶： 你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?

  • 示例 1：
    输入：nums = [3,0,1]
    输出：2
    解释：n = 3，因为有3个数字，所以所有的数字都在范围[0,3]内。2是丢失的数字，因为它没有出现在nums中。
  • 示例 2：
    输入：nums = [0,1]
    输出：2
    解释：n = 2，因为有2个数字，所以所有的数字都在范围[0,2]内。2是丢失的数字，因为它没有出现在nums中。
  • 示例 3：
    输入：nums = [9,6,4,2,3,5,7,0,1]
    输出：8
    解释：n = 9，因为有9个数字，所以所有的数字都在范围[0,9]内。8是丢失的数字，因为它没有出现在nums中。
  • 示例 4：
    输入：nums = [0]
    输出：1
    解释：n = 1，因为有1个数字，所以所有的数字都在范围[0,1]内。1是丢失的数字，因为它没有出现在nums中。

方法一：数学方式

首先求出数组的和，然后再求出前n+1项之和（从0到n），最终求差值，即为缺失的值！

1
2
3
4
#Python
class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        return sum(range(len(nums) + 1)) - sum(nums)

执行耗时:36 ms,击败了98.84% 的Python3用户
内存消耗:14.3 MB,击败了81.49% 的Python3用户

1
2
3
4
5
6
7
8
9
//Java
class Solution {
    public int missingNumber(int[] nums) {
        int sum1 = 0, sum2 = 0;
        for(int i =0; i <= nums.length; i++) sum1 += i;
        for(int num: nums) sum2 += num;
        return sum1 - sum2;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.8 MB, 在所有 Java 提交中击败了75.78% 的用户

方法二：位运算

利用“两个相同的数，使用异或可以相消除”的原理

1
2
3
4
5
6
7
#Python
class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        result = 0
        for i in range(len(nums)):
            result ^= nums[i] ^ i
        return result ^ len(nums)

执行耗时:60 ms,击败了40.05% 的Python3用户
内存消耗:14.6 MB,击败了17.63% 的Python3用户

1
2
3
4
5
6
7
8
//Java
class Solution {
    public int missingNumber(int[] nums) {
        int res = 0;
        for(int i = 0; i < nums.length; i++) res ^= nums[i] ^ i;
        return res ^= nums.length;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了91.43% 的用户

二分法系列

1.阿珂喜欢吃香蕉

第875题：阿珂喜欢吃香蕉
这里总共有 N 堆香蕉，第 i 堆中有piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。 阿珂可以决定她吃香蕉的速度 K （单位：根/小时），每个小时，她将会选择一堆香蕉，从中吃掉 K 根。

如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）。

示例 1：

1
2
输入: piles = [3,6,7,11], H = 8
输出: 4

示例 2：

1
2
输入: piles = [30,11,23,4,20], H = 5
输出: 30

示例 3：

1
2
输入: piles = [30,11,23,4,20], H = 6
输出: 23

提示：

1
2
3
1 <= piles.length <= 10^4
piles.length <= H <= 10^9
1 <= piles[i] <= 10^9

二分查找是计算机科学中最基本、最有用的算法之一。它描述了在有序集合中搜索特定值的过程。一般二分查找由以下几个术语构成：

  • 目标 Target —— 你要查找的值
  • 索引 Index —— 你要查找的当前位置
  • 左、右指示符 Left，Right —— 我们用来维持查找空间的指标
  • 中间指示符 Mid —— 我们用来应用条件来确定我们应该向左查找还是向右查找的索引

在最简单的形式中，二分查找对具有指定左索引和右索引的连续序列进行操作。我们也称之为查找空间。二分查找维护查找空间的左、右和中间指示符，并比较查找目标；如果条件不满足或值不相等，则清除目标不可能存在的那一半，并在剩下的一半上继续查找，直到成功为止。

总结一下一般实现的几个条件：

  • 初始条件：left = 0, right = length-1
  • 终止：left > right
  • 向左查找：right = mid-1
  • 向右查找：left = mid +1

绝大部分 「在递增递减区间中搜索目标值」 的问题，都可以转化为二分查找问题。并且，二分查找的题目，基本逃不出三种：找特定值，找大于特定值的元素（上界），找小于特定值的元素（下界）。

将上面的思想代入到本题，我们要找 “阿珂在 H 小时吃掉所有香蕉的最小速度 K”。那最笨的就是阿珂吃的特别慢，每小时只吃掉 1 根香蕉，然后我们逐渐递增阿珂吃香蕉的速度到 i，刚好满足在 H 小时可以吃掉所有香蕉，此时 i 就是我们要找的最小速度。当然，我们没有这么笨，所以可以想到使用二分的思想来进行优化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#Python
class Solution:
    def minEatingSpeed(self, piles: List[int], H: int) -> int:
        # 最小速度
        low = 1
        # 最大的速度，当然等于吃掉最大一堆的香蕉，毕竟一小时只能吃一堆，再大也没有意义
        high = max(piles)
        def canEat(piles, speed, H):
            sum = 0
            for pile in piles:
                # 向上取整
                if pile % speed > 0:
                    sum += pile // speed + 1
                else:
                    sum += pile // speed
            return sum > H

        while low < high:
            # 中间速度
            mid = (low + high) >> 1
            # 如果超时就往大的方向找，否则往小的方向找
            if canEat(piles, mid, H):
                low = mid + 1
            else:
                high = mid

        return low

执行耗时:372 ms,击败了59.53% 的Python3用户
内存消耗:14.7 MB,击败了9.52% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//Java
class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int low = 1;
        int high = 1;
        for(int pile: piles) high = pile > high? pile: high;
        while(low < high){
            int mid = low + (high - low) / 2;
            if(canEat(piles, mid, h)) low = mid + 1;
            else high = mid;
        }
        return low;
    }

    public boolean canEat(int[] piles, double speed, int h){
        int sum = 0;
        for(int pile: piles){
            sum += Math.ceil(pile / speed);
        }
        return sum > h;
    }
}

执行用时：43 ms, 在所有 Java 提交中击败了10.82% 的用户
内存消耗：39.5 MB, 在所有 Java 提交中击败了80.42% 的用户

2.x的平方根

第69题：x的平方根
计算并返回 x 的平方根，其中 x 是非负整数。由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

整数平方根一定小于等于 x/2 。即有 0 < 整数平方根 <= x/2。所以我们的问题转化为在 [0,x/2] 中找一个特定值，满足二分查找的条件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Python
class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 0:
            return 0
        left = 1
        right = x // 2
        while left < right:
            # +1防止陷入死循环
            mid = (left + right + 1) >> 1
            if mid ** 2 <= x:
                left = mid
            else:
                right = mid - 1
        return left

执行耗时:40 ms,击败了92.37% 的Python3用户
内存消耗:13.6 MB,击败了5.34% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int mySqrt(int x) {
        int l = 1;
        int r = x / 2 + 1;
        while(l < r){
            int mid = l + (r - l) / 2;
            if(x / mid > mid) l = mid + 1;
            else r = mid;
        }
        return x / l < l? l-1: l;
    }
}

执行用时：2 ms, 在所有 Java 提交中击败了46.99% 的用户
内存消耗：35.3 MB, 在所有 Java 提交中击败了95.82% 的用户

牛顿迭代法

1
2
3
4
5
6
7
8
9
10
11
//Java
class Solution {
    public int mySqrt(int x) {
        if(x < 2) return x;
        long a = x;
        while(x / a < a){
            a = (a + x / a) / 2;
        }
        return (int)a;
    }
}

执行用时：2 ms, 在所有 Java 提交中击败了46.99% 的用户
内存消耗：35.6 MB, 在所有 Java 提交中击败了48.99% 的用户

3.第一个错误的版本

第278题：第一个错误的版本
假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例:

1
2
3
4
5
6
7
给定 n = 5，并且 version = 4 是第一个错误的版本。

调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true

所以，4 是第一个错误的版本。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#Python
class Solution:
    def firstBadVersion(self, n):
        """
        :type n: int
        :rtype: int
        """
        left = 1
        right = n
        while left < right:
            mid = (left + right) >> 1
            if isBadVersion(mid):
                right = mid
            else:
                left = mid + 1
        return left

执行耗时:52 ms,击败了5.21% 的Python3用户
内存消耗:13.5 MB,击败了6.31% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int left = 1;
        int right = n;
        while(left < right){
            int mid = left + (right - left) / 2;
            if(isBadVersion(mid)) right = mid;
            else left = mid + 1;
        }
        return left;
    }
}

执行用时：18 ms, 在所有 Java 提交中击败了29.41% 的用户
内存消耗：35.1 MB, 在所有 Java 提交中击败了68.44% 的用户

4.旋转排序数组中的最小值I

第153题：旋转排序数组最小值Ⅰ
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。请找出其中最小的元素。你可以假设数组中不存在重复元素。

示例 1:

1
2
输入: [3,4,5,1,2]
输出: 1

示例 2:

1
2
输入: [4,5,6,7,0,1,2]
输出: 0

无论怎么旋转，我们都可以得到一个结论，首元素 > 尾元素

并且我们已知了首元素值总是大于尾元素，那我们只要找到将其一分为二的那个点（该点左侧的元素都大于首元素，该点右侧的元素都小于首元素），是不是就可以对应找到数组中的最小值。

然后我们通过二分来进行查找，先找到中间节点mid，如果中间元素小于尾元素，我们就把mid向左移动。

如果中间元素大于尾元素，我们就把mid向右移动。

之所以跟尾元素比，是因为测试用例:[11,13,15,17]，算他原地翻转，其结果为11，若跟首元素比，则结果为17导致出错

1
2
3
4
5
6
7
8
9
10
11
12
#Python
class Solution:
    def findMin(self, nums: List[int]) -> int:
        left = 0
        right = len(nums) - 1
        while left < right:
            mid = (left + right) >> 1
            if nums[mid] > nums[-1]:
                left = mid + 1
            else:
                right = mid
        return nums[left]

执行耗时:28 ms,击败了99.24% 的Python3用户
内存消耗:13.7 MB,击败了8.37% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
//Java
class Solution {
    public int findMin(int[] nums) {
        int l = 0, r = nums.length - 1;
        while(l < r){
            int mid = l + (r - l) / 2;
            if(nums[mid] > nums[r]) l = mid + 1;
            else r = mid;
        }
        return nums[l];
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：37.8 MB, 在所有 Java 提交中击败了78.33% 的用户

5.旋转排序数组中的最小值II

第154题：旋转排序数组最小值Ⅱ
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。请找出其中最小的元素。 注意数组中可能存在重复的元素。

示例 1：

1
2
输入: [1,3,5]
输出: 1

示例 2：

1
2
输入: [2,2,2,0,1]
输出: 0

说明：

相对比昨天题目而言，其实只是多了nums[mid] 等于 nums[right] 时的额外处理。

可以看到在 nums[mid] 等于 nums[right] 时的情况下，我们只多了一个 right-1 的操作。

因为 mid 和 right 相等时，最小值既可能在左边，又可能在右边，所以此时自然二分思想作废，咱们就砍掉一个右边界。说白了，就是让子弹再飞一会儿。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#Python
class Solution:
    def findMin(self, nums: List[int]) -> int:
        left = 0
        right = len(nums) - 1
        while left < right:
            mid = (left + right) >> 1
            if nums[mid] > nums[right]:
                left = mid + 1
            elif nums[mid] < nums[right]:
                right = mid
            else:
                right -= 1
        return nums[left]

执行耗时:48 ms,击败了23.32% 的Python3用户
内存消耗:13.7 MB,击败了27.84% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int findMin(int[] nums) {
        int l = 0, r = nums.length - 1;
        while(l < r){
            int mid = l + (r - l) / 2;
            if(nums[mid] > nums[r]) l = mid + 1;
            else if(nums[mid] < nums[r]) r = mid;
            else r--;
        }
        return nums[l];
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了27.61% 的用户
内存消耗：38.2 MB, 在所有 Java 提交中击败了73.68% 的用户

6.供暖器

第475题：供暖器
冬季已经来临。你的任务是设计一个有固定加热半径的供暖器向所有房屋供暖。现在，给出位于一条水平线上的房屋和供暖器的位置，找到可以覆盖所有房屋的最小加热半径。所以，你的输入将会是房屋和供暖器的位置。你将输出供暖器的最小加热半径。

说明:

  • 给出的房屋和供暖器的数目是非负数且不会超过 25000。
  • 给出的房屋和供暖器的位置均是非负数且不会超过10^9。
  • 只要房屋位于供暖器的半径内(包括在边缘上)，它就可以得到供暖。
  • 所有供暖器都遵循你的半径标准，加热的半径也一样。

示例 1:

1
2
3
输入: [1,2,3],[2]
输出: 1
解释: 仅在位置2上有一个供暖器。如果我们将加热半径设为1，那么所有房屋就都能得到供暖。

示例 2:

1
2
3
输入: [1,2,3,4],[1,4]
输出: 1
解释: 在位置1, 4上有两个供暖器。我们需要将加热半径设为1，这样所有房屋就都能得到供暖。

我们要对任意一个房屋供暖，要么用前面的暖气，要么用后面的暖气，两者之间取最近的，这就是距离。同时，如果要覆盖到所有的房屋，我们要选择上述距离中最大的一段，这就是最小的加热半径。

第一层：遍历所有的房子，第二层：遍历加热器，找出距离该房子的最小距离。但是我们其实可以通过二分搜索来优化这个过程。

方法一：暴力法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#Python
class Solution:
    def findRadius(self, houses: List[int], heaters: List[int]) -> int:
        houses.sort()
        heaters.sort()
        # 防止供暖器只有一个的情况
        heaters = [float("-inf")] + heaters + [float("inf")]
        i = 1
        res = 0
        for house in houses:
            while i < len(heaters) - 1 and house > heaters[i]:
                i += 1
            res = max(res, min(heaters[i] - house, house - heaters[i - 1]))
        return res

执行耗时:140 ms,击败了92.39% 的Python3用户
内存消耗:16.1 MB,击败了85.24% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//Java
class Solution {
    public int findRadius(int[] houses, int[] heaters) {
        Arrays.sort(houses);
        Arrays.sort(heaters);
        int[] nheaters = new int[heaters.length+2];
        nheaters[0] = Integer.MIN_VALUE;
        nheaters[nheaters.length-1] = Integer.MAX_VALUE;
        System.arraycopy(heaters, 0, nheaters, 1, heaters.length);
        int index = 1;
        double res = 0;
        for(double house: houses){
            while(index < nheaters.length - 1 && house > nheaters[index]) index++;
            res = Math.max(res, Math.min(nheaters[index] - house, house - nheaters[index-1]));
        }
        return (int) res;
    }
}

执行用时：9 ms, 在所有 Java 提交中击败了89.71% 的用户
内存消耗：41.2 MB, 在所有 Java 提交中击败了92.17% 的用户

方法二：二分法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#Python
class Solution:
    def findRadius(self, houses: List[int], heaters: List[int]) -> int:
        houses.sort()
        # 找到每个房屋位置所需要的最小半径的最大值
        res = 0
        # 防止供暖器只有一个的情况
        heaters = [-float("inf")] + sorted(heaters) + [float("inf")]
        # 每个屋子都要被覆盖到
        for house in houses:
            # 每个屋子都要找到1个离他最近的heater，这里用二分法改进
            left, right = 0, len(heaters)-1
            # 找不小于house的第一个heater值
            while left < right:
            	# 应该写mid=left+((right-left)>>1)，因为位运算的优先级不如加法运算
                mid = left + ((right - left) >> 1)
                if house > heaters[mid]:
                    left = mid + 1
                else:
                    right = mid
            # house夹在heaters[left-1] heater[left]中间
            res = max(res, min(house - heaters[left - 1], heaters[left] - house))
        return res

执行耗时:252 ms,击败了86.09% 的Python3用户
内存消耗:15.9 MB,击败了93.07% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int findRadius(int[] houses, int[] heaters) {
        double res = 0;
        Arrays.sort(heaters);
        int[] nheaters = new int[heaters.length+2];
        nheaters[0] = Integer.MIN_VALUE;
        nheaters[nheaters.length-1] = Integer.MAX_VALUE;
        System.arraycopy(heaters, 0, nheaters, 1, heaters.length);
        for(double house: houses){
            int left = 0, right = nheaters.length;
            while (left < right){
                int mid = left + (right - left) / 2;
                if(house > nheaters[mid]) left = mid + 1;
                else right = mid;
            }
            res = Math.max(res, Math.min(nheaters[left] - house, house - nheaters[left-1]));
        }
        return (int) res;
    }
}

执行用时：23 ms, 在所有 Java 提交中击败了39.37% 的用户
内存消耗：41.3 MB, 在所有 Java 提交中击败了84.79% 的用户

其他补充题目

1.螺旋矩阵I

第54题：螺旋矩阵
定一个包含 m x n 个元素的矩阵（m 行, n 列），请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例 1:

1
2
3
4
5
6
7
输入:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]

示例 2:

1
2
3
4
5
6
7
输入:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]

只有我们能找到边界（边界包括：1、数组的边界 2、已经访问过的元素），才可以通过“右，下，左，上”的方向来进行移动。同时，每一次碰壁，就可以调整到下一个方向。

我们首先对其设置好四个边界:

1
2
3
4
up := 0
down := len(matrix) - 1
left := 0
right := len(matrix[0]) - 1

同时，我们定义x和y，来代表行和列。

然后我们从第一个元素开始行军（y=left），完成第一行的遍历，直到碰壁。（y<=right）

下面关键的一步来了，因为第一行已经走过了，我们将上界下调 （up++），同时转弯向下走。

直到碰到底部时（x<=down），我们将右界左调（right—），转弯向左走。

后面向左和向上，分别完成下界上调（down—和左界右调（left++）。

最后，对剩下的矩阵重复整个过程，直到上下、左右的壁与壁碰在一起 （up <= down && left <= right，这是避免碰壁的条件）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#Python
class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        result = []
        left, right, up, down = 0, len(matrix[0]) - 1, 0, len(matrix) - 1
        x, y = 0, 0
        while left <= right and up <= down:
            for y in range(left, right+1):
                if left <= right and up <= down:
                    result.append(matrix[x][y])
            up += 1

            for x in range(up, down+1):
                if left <= right and up <= down:
                    result.append(matrix[x][y])
            right -= 1

            for y in range(right, left-1, -1):
                if left <= right and up <= down:
                    result.append(matrix[x][y])
            down -= 1

            for x in range(down, up-1, -1):
                if left <= right and up <= down:
                    result.append(matrix[x][y])
            left += 1

        return result

执行耗时:40 ms,击败了60.32% 的Python3用户
内存消耗:13.3 MB,击败了73.96% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> res = new ArrayList<>();
        int left = 0, right = matrix[0].length - 1, up = 0, down = matrix.length - 1;
        while(left <= right && up <= down){
            for(int y = left; y <= right; y++) res.add(matrix[up][y]);
            up++;
            for(int x = up; x <= down; x++) res.add(matrix[x][right]);
            right--;
            if(up > down) break;
            for(int y = right; y >= left; y--) res.add(matrix[down][y]);
            down--;
            if(left > right) break;
            for(int x = down; x >= up; x--) res.add(matrix[x][left]);
            left++;
        }
        return res;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.5 MB, 在所有 Java 提交中击败了76.13% 的用户

2.只有两个键的键盘

第650题：只有两个键的键盘
最初在一个记事本上只有一个字符 ‘A’ 。你每次可以对这个记事本进行两种操作：Copy All (复制全部) : 你可以复制这个记事本中的所有字符(部分的复制是不允许的)。Paste (粘贴) : 你可以粘贴你上一次复制的字符。

给定一个数字 n 。你需要使用最少的操作次数，在记事本中打印出恰好 n 个 ‘A’。输出能够打印出 n 个 ‘A’ 的最少操作次数。

示例 1:

1
2
3
4
5
6
7
输入: 3
输出: 3
解释:
最初, 我们只有一个字符 'A'。
第 1 步, 我们使用 Copy All 操作。
第 2 步, 我们使用 Paste 操作来获得 'AA'。
第 3 步, 我们使用 Paste 操作来获得 'AAA'。

说明:

n 的取值范围是 [1, 1000] 。

本题的思路，在于想明白复制和粘贴过程中的规律，找到如何组成N个A的最小操作数。

我们从最简单的开始分析，假如我们给定数字为1，那啥也不用做，因为面板上本来就有一个A。

假如我们给定数字为2，那我们需要做C-P，共计2次操作来得到。

假如我们给定数字为3，那我们需要做C-P-P，共计3次操作来得到。

假如我们给定数字为4，我们发现好像变得不一样了。因为我们有两种方法都可以得到目标。（C-P-C-P）

或者（C-P-P-P）

但是需要的步骤还是一样。

好了，到这里为止，STOP！通过上面的分析，我们至少可以观察出：如果 i 为质数，那么 i 是多少，就需要粘贴多少次。即：素数次数为本身的结论。如 两个A = 2，三个A = 3，五个A = 5。

那对于合数又该如何分析呢？（自然数中除能被1和本身整除外,还能被其他的数整除的数）这里我们直接给出答案：合数的次数为将其分解质因数的操作次数的和。 解释一下，这是个啥意思？举个例子：

比如30，可以分解为：3*2*5。什么意思呢？我们演示一遍：首先复制1，进行2次粘贴得到3。然后复制3，进行1次粘贴得到6。然后复制6，进行4次粘贴得到30。总共需要（CPPCPCPPPP）

注意：这里由于每一次都需要进行一次复制，所以直接就等于分解质因数的操作次数的和。并且分解的顺序，不会影响到结果。

综合上面的分析，我们得出分析结果：

1、质数次数为其本身。

2、合数次数为将其分解到所有不能再分解的质数的操作次数的和。

1
2
3
4
5
6
7
8
9
#Python
class Solution:
    def minSteps(self, n: int) -> int:
        res = 0
        for i in range(2, n+1):
            while n % i == 0:
                res += i
                n /= i
        return res

执行耗时:36 ms,击败了91.24% 的Python3用户
内存消耗:13.6 MB,击败了19.97% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int minSteps(int n) {
        int res = 0;
        for(int i = 2; i <= n; i++){
            while(n % i == 0){
                res += i;
                n /= i;
            }
        }
        return res;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.4 MB, 在所有 Java 提交中击败了43.12% 的用户

3.24点游戏

第679题：24点游戏
你有 4 张写有 1 到 9 数字的牌。你需要判断是否能通 *，/，+，-，(，) 的运算得到 24 。

示例 1:

1
2
3
输入: [4, 1, 8, 7]
输出: True
解释: (8-4) * (7-1) = 24

示例 2:

1
2
输入: [1, 2, 1, 2]
输出: False

注意:

​ 1、除法运算符 / 表示实数除法，而不是整数除法。例如 4 / (1 - 2/3) = 12 。

​ 2、每个运算符对两个数进行运算。特别是我们不能用 - 作为一元运算符。例如，[1, 1, 1, 1] 作为输入时，表达式 -1 - 1 - 1 - 1 是不允许的。

​ 3、你不能将数字连接在一起。例如，输入为 [1, 2, 1, 2] 时，不能写成 12 + 12 。

拿到题目，第一反应就可以想到暴力求解。如果我们要判断给出的4张牌是否可以通过组合得到24，那我们只需找出所有的可组合的方式进行遍历。

4个数字，3个操作符，外加括号，基本目测就能想到组合数不会大到超出边界。所以，我们只要把他们统统列出来，不就可以进行求解了吗?

但是这个方法写的正确吗？其实不对！因为在计算机中，实数在计算和存储过程中会有一些微小的误差，对于一些与零作比较的语句来说，有时会因误差而导致原本是等于零但结果却小于或大于零之类的情况发生，所以常用一个很小的数 1e-6 代替 0，进行判读！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#Python
class Solution:
    def judgePoint24(self, nums: List[int]) -> bool:
        op = [lambda x, y: x + y, lambda x, y: x - y, lambda x, y: x * y,
              lambda x, y: x / y if y != 0 else float('inf')]
        # 返回可迭代对象的所有数学全排列方式
        for a, b, c, d in itertools.permutations(nums):
            # product(list1, list2) 依次取出list1中的每1个元素，与list2中的每1个元素，组成元组，
            # 然后，将所有的元组组成一个列表，返回。
            for f, g, h in itertools.product(op, repeat=3):
                if -1e-6 < f(g(h(a, b), c), d) - 24 < 1e-6 \
                        or -1e-6 < f(g(a, h(b, c)), d) - 24 < 1e-6 \
                        or -1e-6 < f(g(a, b), h(c, d)) - 24 < 1e-6 \
                        or -1e-6 < f(a, g(h(b, c), d)) - 24 < 1e-6 \
                        or -1e-6 < f(a, g(b, h(c, d))) - 24 < 1e-6:
                    return True
        return False

执行耗时:68 ms,击败了92.38% 的Python3用户
内存消耗:13.3 MB,击败了68.61% 的Python3用户

可以通过回溯的方法遍历所有不同的可能性。具体做法是，使用一个列表存储目前的全部数字，每次从列表中选出 2 个数字，再选择一种运算操作，用计算得到的结果取代选出的 2 个数字，这样列表中的数字就减少了 1 个。重复上述步骤，直到列表中只剩下 1 个数字，这个数字就是一种可能性的结果，如果结果等于 24，则说明可以通过运算得到 24。如果所有的可能性的结果都不等于 24，则说明无法通过运算得到 24。

实现时，有一些细节需要注意。

  • 除法运算为实数除法，因此结果为浮点数，列表中存储的数字也都是浮点数。在判断结果是否等于 24 时应考虑精度误差，这道题中，误差小于 10−6 可以认为是相等。

  • 进行除法运算时，除数不能为 0，如果遇到除数为 0 的情况，则这种可能性可以直接排除。由于列表中存储的数字是浮点数，因此判断除数是否为 0 时应考虑精度误差，这道题中，当一个数字的绝对值小于 10−6 时，可以认为该数字等于 0。

还有一个可以优化的点。

  • 加法和乘法都满足交换律，因此如果选择的运算操作是加法或乘法，则对于选出的 2 个数字不需要考虑不同的顺序，在遇到第二种顺序时可以不进行运算，直接跳过。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
//Java
class Solution {
    //目标值
    static final int TARGET = 24;
    //误差
    static final double EPSILON = 1e-6;
    //四种运算
    static final int ADD = 0, MULTIPLY = 1, SUBTRACT = 2, DIVIDE = 3;

    public boolean judgePoint24(int[] nums) {
        List<Double> list = new ArrayList<Double>();
        for (int num : nums) {
            list.add((double) num);
        }
        return solve(list);
    }
    
    //回溯
    public boolean solve(List<Double> list) {
        //列表为空，返回false
        if (list.size() == 0) return false;
        //组合的结果是否为target
        if (list.size() == 1) return Math.abs(list.get(0) - TARGET) < EPSILON;
        int size = list.size();
        //从当前列表中选出两个数
        for (int i = 0; i < size; i++) {
            for (int j = 0; j < size; j++) {
                if (i != j) {
                    //新建列表
                    List<Double> list2 = new ArrayList<Double>();
                    //选出的两个数外的数，仍存入列表
                    for (int k = 0; k < size; k++) {
                        if (k != i && k != j) list2.add(list.get(k));
                    }
                    //选择其中一种运算
                    for (int k = 0; k < 4; k++) {
                        //加法和乘法都满足交换律，因此如果选择的运算操作是加法或乘法，则对于选出的数字不需要考虑不同的顺序
                        //在遇到第二种顺序时可以不进行运算，直接跳过
                        if (k < 2 && i > j) {
                            continue;
                        }
                        //将两个数的运算结果存入新数组
                        if (k == ADD) {
                            list2.add(list.get(i) + list.get(j));
                        } else if (k == MULTIPLY) {
                            list2.add(list.get(i) * list.get(j));
                        } else if (k == SUBTRACT) {
                            list2.add(list.get(i) - list.get(j));
                        } else if (k == DIVIDE) {
                            //排除除数为0的情况
                            if (Math.abs(list.get(j)) < EPSILON) {
                                continue;
                            } else {
                                list2.add(list.get(i) / list.get(j));
                            }
                        }
                        //递归，从新数组中继续选取两个数
                        if (solve(list2)) return true;
                        //回溯
                        list2.remove(list2.size() - 1);
                    }
                }
            }
        }
        return false;
    }
}

执行用时：5 ms, 在所有 Java 提交中击败了67.43% 的用户
内存消耗：38.1 MB, 在所有 Java 提交中击败了62.84% 的用户

4.飞机座位分配概率

第1227题：飞机座位分配概率
有 n 位乘客即将登机，飞机正好有 n 个座位。第一位乘客的票丢了，他随便选了一个座位坐下。

剩下的乘客将会：

  • 如果他们自己的座位还空着，就坐到自己的座位上，
  • 当他们自己的座位被占用时，随机选择其他座位

第 n 位乘客坐在自己的座位上的概率是多少？

示例 1：

1
2
3
输入：n = 1
输出：1.00000
解释：第一个人只会坐在自己的位置上。

示例 2：

1
2
3
输入: n = 2
输出: 0.50000
解释：在第一个人选好座位坐下后，第二个人坐在自己的座位上的概率是 0.5。

一个位置一个人，一屁股蹲下，概率100%，这没啥可说的。

两个位置两个人，第一个人已经坐下，要么坐对了，要么坐错了。所以第二个人坐在自己位置上的概率是50%。

重点来了，三个位置三个人，第一个一屁股坐下，有三种坐法。

如果恰好第一个人坐到了自己的座位上（1/3），那这种情况下，第二个人也就可以直接坐在自己的座位上，第三个人一样。所以此时第三人坐在自己座位上的可能性是 100%。

如果第一个人占掉了第二个人的位置（1/3）。 此时第二人上来之后，要么坐在第一人的位置上，要么坐在第三人的位置上。（1/2）所以，在这种情况下，第三人的座位被占的可能性是 1/3*1/2=1/6。

那假如第一人直接一屁股坐在第三人的座位上，此时第三人的座位被占的可能性就是第一人选择第三人座位的可能性。（1/3）

所以，如果三个座位三个人，第三个人坐到自己位置上的概率就是：1/3 1/1 + 1/3 1/2 + 1/3 * 0 = 1/2

而对于 n>3 的情况，我们参照 3 个座位时进行分析：

  • 如果第1个乘客选择第1个座位，那么第n个人选择到第n个座位的可能性就是100%。(1/n)
  • 如果第1个乘客选择了第n个座位，那么第n个人选择第n个座位的可能性就是0。(0)
  • 而对于第 1 个乘客选择除了第一个和第 n 个座位之外的座位k (1<k<n)，就会导致有可能出现，前 n-1 位乘客占第 n 位乘客的概率出现。

第一二种情况都好说，对于第三种情况。因为此时第k个座位被占用，于第 k 个乘客而言，他又会面临和第一个乘客一样的选择。相当于乘客1将问题转移到了第k个乘客身上，等同于本次选择无效！且这个过程会一直持续到没有该选项。于是乎，对于第 n 个人，他最后将只有两个选项：1、自己的 2、第一个人。所以对于n>=3 的情况，等同于 n=2，全部的概率都为 1/2。

如果还是不能理解的小伙伴，可以这样想。登机时座位被占的乘客 ，其实相当于和上一位坐错的乘客交换了身份。直到完成终止条件（坐对位置 或者 坐到最后一个位置），否则该交换将一直进行下去。所以第n位乘客，坐到第n个位置，自然还是 1/2。

1
2
3
4
5
6
7
#Python
class Solution:
    def nthPersonGetsNthSeat(self, n: int) -> float:
        if n == 1:
            return 1
        else:
            return 0.5

执行耗时:44 ms,击败了46.71% 的Python3用户
内存消耗:13.5 MB,击败了37.32% 的Python3用户

1
2
3
4
5
6
7
//Java
class Solution {
    public double nthPersonGetsNthSeat(int n) {
        if(n == 1) return 1.0;
        else return 0.5;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.3 MB, 在所有 Java 提交中击败了96.75% 的用户

5.水分子的产生

第1117题：水分子的产生
现在有两种线程，氢 oxygen 和氧 hydrogen，你的目标是组织这两种线程来产生水分子。

存在一个屏障（barrier）使得每个线程必须等候直到一个完整水分子能够被产生出来。

氢和氧线程会被分别给予 releaseHydrogen 和 releaseOxygen 方法来允许它们突破屏障。

这些线程应该三三成组突破屏障并能立即组合产生一个水分子。

你必须保证产生一个水分子所需线程的结合必须发生在下一个水分子产生之前。

换句话说:

如果一个氧线程到达屏障时没有氢线程到达，它必须等候直到两个氢线程到达。

如果一个氢线程到达屏障时没有其它线程到达，它必须等候直到一个氧线程和另一个氢线程到达。

书写满足这些限制条件的氢、氧线程同步代码。

示例 1:

1
2
3
输入: "HOH"
输出: "HHO"
解释: "HOH" 和 "OHH" 依然都是有效解。

示例 2:

1
2
3
输入: "OOHHHH"
输出: "HHOHHO"
解释: "HOHHHO", "OHHHHO", "HHOHOH", "HOHHOH", "OHHHOH", "HHOOHH", "HOHOHH" 和 "OHHOHH" 依然都是有效解。

限制条件:

  • 输入字符串的总长将会是 3n, 1 ≤ n ≤ 50；
  • 输入字符串中的 “H” 总数将会是 2n；
  • 输入字符串中的 “O” 总数将会是 n。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from threading import Semaphore

class H2O:
    def __init__(self):
        self.h = Semaphore(2)
        self.o = Semaphore(0)
        self.h_num = 0

    def hydrogen(self, releaseHydrogen: 'Callable[[], None]') -> None:
        self.h.acquire(1)
        # releaseHydrogen() outputs "H". Do not change or remove this line.
        releaseHydrogen()
        self.h_num += 1
        if self.h_num == 2:
            self.h_num = 0
            self.o.release(1)

    def oxygen(self, releaseOxygen: 'Callable[[], None]') -> None:
        self.o.acquire(2)
        # releaseOxygen() outputs "O". Do not change or remove this line.
        releaseOxygen()
        self.h.release(2)

执行用时：40 ms, 在所有 Python3 提交中击败了92.16% 的用户
内存消耗：15.4 MB, 在所有 Python3 提交中击败了81.37% 的用户

Semaphore是 synchronized 的加强版，作用是控制线程的并发数量。可以通过 acquire 和 release 来进行类似 lock 和 unlock 的操作。

1
2
3
4
//请求一个信号量，这时候信号量个数-1，当减少到0的时候，下一次acquire不会再执行，只有当执行一个release()的时候，信号量不为0的时候才可以继续执行acquire
void acquire()
//释放一个信号量，这时候信号量个数+1，
void release();

h每获取一次释放一个o许可，o每次获取两个许可（即2次h后执行一次o）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Java
class H2O {

    private Semaphore h = new Semaphore(2);
    private Semaphore o = new Semaphore(0);
    public H2O() {
        
    }

    public void hydrogen(Runnable releaseHydrogen) throws InterruptedException {
		h.acquire(1);
        // releaseHydrogen.run() outputs "H". Do not change or remove this line.
        releaseHydrogen.run();
        o.release(1);
    }

    public void oxygen(Runnable releaseOxygen) throws InterruptedException {
        o.acquire(2);
        // releaseOxygen.run() outputs "O". Do not change or remove this line.
		releaseOxygen.run();
        h.release(2);
    }
}

执行用时：19 ms, 在所有 Java 提交中击败了78.17% 的用户
内存消耗：39.9 MB, 在所有 Java 提交中击败了87.10% 的用户

6.救生艇

第881题：救生艇
第 i 个人的体重为 people[i]，每艘船可以承载的最大重量为 limit。每艘船最多可同时载两人，但条件是这些人的重量之和最多为 limit。返回载到每一个人所需的最小船数。(保证每个人都能被船载)。

示例 1：

1
2
3
输入：people = [1,2], limit = 3
输出：1
解释：1 艘船载 (1, 2)

示例 2：

1
2
3
输入：people = [3,2,2,1], limit = 3
输出：3
解释：3 艘船分别载 (1, 2), (2) 和 (3)

示例 3：

1
2
3
输入：people = [3,5,3,4], limit = 5
输出：4
解释：4 艘船分别载 (3), (3), (4), (5)

提示：

  • 1 <= people.length <= 50000
  • 1 <= people[i] <= limit <= 30000

这不是一道算法题，这是一个脑筋急转弯。

一个船最多可以装两个人，并且不能把船压垮。同时要求把这些人可以统统装下的最小船数。用脚趾头也可以想到，我们需要尽最大努力的去维持一个床上得有两个人。。哦，不，船上。这是什么思想？Bingo，贪心。

思路很简单：

  1. 我们首先需要让这些人根据体重进行排序。
  2. 同时维护两个指针，每次让最重的一名上船，同时让最轻的也上船。（因为最重的要么和最轻的一起上船。要么就无法配对，只能自己占用一艘船的资源）
1
2
3
4
5
6
7
8
9
10
11
12
13
#Python
class Solution:
    def numRescueBoats(self, people: List[int], limit: int) -> int:
        people.sort()
        ans = 0
        i = 0
        j = len(people) - 1
        while i <= j:
            if people[i] + people[j] <= limit:
                i += 1
            j -= 1
            ans += 1
        return ans

执行耗时:504 ms,击败了97.01% 的Python3用户
内存消耗:20.3 MB,击败了29.93% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//Java
class Solution {
    public int numRescueBoats(int[] people, int limit) {
        int ans = 0;
        Arrays.sort(people);
        int l = 0, r = people.length -1;
        while(l <= r){
            if(people[l] + people[r] <= limit) l++;
            r--;
            ans++;
        }
        return ans;
    }
}

执行用时：17 ms, 在所有 Java 提交中击败了96.78% 的用户
内存消耗：47.2 MB, 在所有 Java 提交中击败了77.37% 的用户

7.25匹马的经典问题

25匹马的问题
有一个赛场上共有25匹马，赛场有5个跑道，不使用计时器进行比赛（也就是每次比赛只能得到本次的比赛的顺序）

试问最少比多少场才能选出最快的三匹马？并给出分析过程！

分析过程：

  • 5次：首先我们把25匹马分成5组（A、B、C、D、E），跑上五次，得到每组的第一名。

  • 1次：然后我们让这5个第一名跑上一次，得到其中的前三名。注意：这里就可以得到所有马中跑的最快的第一名A1了。并且，D1和E1所在的组可以直接淘汰。第二名和第三名一定不会在其中产生！

  • 1次：因为我们已经跑出了第一名，所以A1不需要再参加比赛，同时，D1和E1所在的组已经淘汰。C1作为第三组的第一名，C组不会有跑的比C1快的。而B2有可能是比C1跑的快的第三名。同理，A2和A3也有可能是比B1和B2跑的快的。所以第7次比赛，我们让A2，A3，B1，B2，C1来一起完成。

最终，我们通过7次比赛，得到25匹马中的前三名。

升级版本

还是25匹马，如果我们要找到其中跑的最快的前五名，最少需要比赛几次呢？（这里我想说一下，我看到网上有不少地方把这个题讲错了，所以不会的同学建议还是认真看一看）

在上面的的分析中，我们已经明确了第一名。但是第二名和第三名，是可以在A2-A3-B1-B2-C1中产生的，我们需要分别进行讨论。

  • 假若二三名分别为：A2，A3

对于这种情况，第四名可能是A4，此时第五名是A5或者B1。第四名也可能是B1，此时第五名是B2或者C1。所以我们只需要让［A4，B1，A5，B2，C1］参加一次比赛，就可以得到前五名。

  • 假若二三名分别为：A2，B1

对于这种情况，第四名可能是A3、B2、C1。假设第4名为A3，第5名可能为A4、B2、C1。假设第4名为B2，第5名可能为A3、B3、C1。假设第4名为C1，第5名可能为A3、B2、C2、D1。此时我们需要至少两次比赛，才能在［A3，A4，B2，B3，C1，C2，D1］中找到第四名和第五名，所以就需要9次。

其他的可能性还有：

  • 假若二三名分别为：B1，A2
  • 假若二三名分别为：B1，B2
  • 假若二三名分别为：B1，C1

上面这三种情况分析的方法一致，就不一一说明了，大概的思路就是，我们需要根据第三名，分析出可能的第四名。再根据第四名，分析出对应情况下的第五名。最终再在这些马匹里，抉择出真正的第四名和第五名。

因为题中问的是最少比多少场可以跑出前五名。所以根据分析，假如第二名和第三名是A2和A3的话，只需要8次就可以跑出前五名。最少次数是8。（这个题目其实是不严谨的，所以如果有面试官问到这个题，最好是给出所有可能性的推导过程）

8.灯泡开关

第319题：开关灯泡
初始时有 n 个灯泡关闭。第 1 轮，你打开所有的灯泡。第 2 轮，每两个灯泡关闭一次。第 3 轮，每三个灯泡切换一次开关（如果关闭则开启，如果开启则关闭）。第 i 轮，每 i 个灯泡切换一次开关。对于第 n 轮，你只切换最后一个灯泡的开关。找出 n 轮后有多少个亮着的灯泡。

示例:

1
2
3
4
5
6
7
8
9
输入: 3
输出: 1 
解释: 
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭]. 

你应该返回 1，因为只有一个灯泡还亮着。

这是一道难度评定为困难的题目。但是，其实这并不是一道算法题，而是一个脑筋急转弯。只要我们模拟一下开关灯泡的过程，大家就会瞬间get，一起来分析一下：

我们模拟一下n从1到12的过程。在第一轮，你打开了12个灯泡：

因为对于大于n的灯泡你是不care的，所以我们用黑框框表示：

然后我们列出n从1-12的过程中所有的灯泡示意图：

可以得到如下表格：

观察一下，这是什么？观察不出来，咱们看看这个：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//go
func main() {
    for n := 1; n <= 12; n++ {
        fmt.Println("n=", n, "\t灯泡数\t", math.Sqrt(float64(n)))
    }
}
//print
n= 1     灯泡数  1
n= 2     灯泡数  1.4142135623730951
n= 3     灯泡数  1.7320508075688772
n= 4     灯泡数  2
n= 5     灯泡数  2.23606797749979
n= 6     灯泡数  2.449489742783178
n= 7     灯泡数  2.6457513110645907
n= 8     灯泡数  2.8284271247461903
n= 9     灯泡数  3
n= 10     灯泡数  3.1622776601683795
n= 11     灯泡数  3.3166247903554
n= 12     灯泡数  3.4641016151377544

没错，只要我们对n进行开方，就可以得到最终的灯泡数。根据分析，得出代码：

1
2
3
4
#Python
class Solution:
    def bulbSwitch(self, n: int) -> int:
        return int(sqrt(n))

执行耗时:40 ms,击败了60.08% 的Python3用户
内存消耗:13.6 MB,击败了7.43% 的Python3用户

1
2
3
4
5
class Solution {
    public int bulbSwitch(int n) {
        return (int) Math.sqrt(n);
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.1 MB, 在所有 Java 提交中击败了71.93% 的用户

证明如下：

约数，又称因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a。a称为b的倍数，b称为a的约数。

从我们观察可以发现，如果一个灯泡有奇数个约数，那么最后这个灯泡一定会亮着。

什么，你问我奇数是什么？奇数（odd）指不能被2整除的整数 ，数学表达形式为：2k+1， 奇数可以分为正奇数和负奇数。

所以其实我们是求，从1-n有多少个数的约数有奇数个。而有奇数个约数的数一定是完全平方数。 这是因为，对于数n，如果m是它的约数，则n/m也是它的约数，若m≠n/m，则它的约数是以m、n/m的形式成对出现的。而m＝n/m成立且n/m是正整数时，n是完全平方数，而它有奇数个约数。

我们再次转化问题，求1-n有多少个数是完全平方数。

什么，你又不知道什么是完全平方数了？完全平方指用一个整数乘以自己例如1×1，2×2，3×3等，依此类推。若一个数能表示成某个整数的平方的形式，则称这个数为完全平方数。

到这里，基本就很明朗了。剩下的，我想不需要再说了吧！

9.三门问题

三门问题
参赛者的面前有三扇关闭着的门，其中一扇的后面是天使，选中后天使会达成你的一个愿望，而另外两扇门后面则是恶魔，选中就会死亡。

当你选定了一扇门，但未去开启它的时候，上帝会开启剩下两扇门中的一扇，露出其中一只恶魔。（上帝是全能的，必会打开恶魔门）随后上帝会问你要不要更换选择，选另一扇仍然关着的门。

按照常理，参赛者在做出最开始的决定时，对三扇门后面的事情一无所知，因此他选择正确的概率是1/3，这个应该大家都可以想到。

接下来，主持人排除掉了一个错误答案（有恶魔的门），于是剩下的两扇门必然是一扇是天使，一扇是恶魔，那么此时无论选择哪一扇门，胜率都是1/2，依然合乎直觉。

所以你作为参赛者，你会认为换不换都无必要，获胜概率均为1/2。但是，真的是这样吗？

正确的答案是，如果你选择了换，碰见天使的概率会高达2/3，而不不换的话，碰见天使的概率只有1/3。 怎么来的？

我们用一个很通俗的方法，能让你一听就懂。首先刚开始选择的一扇门的概率为1/3，而另外两扇门的总概率为2/3。


现在上帝打开了其中一扇为恶魔的门，我们知道这个门后面不会再有天使，所以相当于这部分概率被第三个门持有。


剩下的那扇门的概率（2/3）相当于刚开始选择的门（1/3）的二倍。所以我们得换。

如果还没有听懂。我们可以假设有一百扇门，里边有99只都是恶魔。现在你随机选择一扇门，选择到天使的概率是1/100。


这时，上帝打开其中的98扇，里边都是恶魔。这时候就相当于99/100的概率都集中在了另一扇门里。自然，我们需要选择换

代码证明
为了验证结果，我用代码跑了一百万次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func main() { 
    //换门遇见天使的次数和不换门遇见天使的次数     changeAngelCount, unchangeAngelCount := 0, 0     for i := 0; i < 1000000; i++ { 
        //门的总数 
        doors := []int{0, 1, 2} 
        //天使门和选中的门         angelDoor, selectedDoor := rand.Intn(3), rand.Intn(3) 
        //上帝移除一扇恶魔门
        for j := 0; j < len(doors); j++ {
            if doors[j] != selectedDoor && doors[j] != angelDoor {
                doors = append(doors[:j], doors[j+1:]...)
                break
            }
        }
        //统计        
        if selectedDoor == angelDoor {
            unchangeAngelCount++
        } else {
            changeAngelCount++
        }
    }
    fmt.Println("不换门遇见天使次数:", unchangeAngelCount, "比例：", (float32(unchangeAngelCount) / 1000000))
    fmt.Println("换门遇见天使次数:", changeAngelCount, "比例：", (float32(changeAngelCount) / 1000000))
}

执行结果为：

10.猜数字游戏

第299题：猜数字（Bulls and Cows）游戏
你写下一个数字让你的朋友猜。每次他猜测后，你给他一个提示，告诉他有多少位数字和确切位置都猜对了（称为“Bulls”, 公牛），有多少位数字猜对了但是位置不对（称为“Cows”, 奶牛）。你的朋友将会根据提示继续猜，直到猜出秘密数字。

请写出一个根据秘密数字和朋友的猜测数返回提示的函数，用 A 表示公牛，用 B 表示奶牛。

请注意秘密数字和朋友的猜测数都可能含有重复数字。

示例 1:

1
2
3
输入: secret = "1807", guess = "7810"
输出: "1A3B"
解释: 1 公牛和 3 奶牛。公牛是 8，奶牛是 0, 1 和 7。

示例 2:

1
2
3
输入: secret = "1123", guess = "0111"
输出: "1A1B"
解释: 朋友猜测数中的第一个 1 是公牛，第二个或第三个 1 可被视为奶牛。

说明: 你可以假设秘密数字和朋友的猜测数都只包含数字，并且它们的长度永远相等。

基本拿到题目，我们就能想到可以使用hashmap进行求解，一起来分析一下。

  • 因为secret数字和guess数字长度相等，所以我们遍历secret数字。
  • 如果当前索引两个数字相同，就将公牛数加1。
  • 如果不相同，我们将secret和guess当前索引位置处的数字通过map记录下来，统计他们出现的次数。当然，之前我们讲过。有限的map，比如数字 0-10，字母 a-z，都可以通过数组来进行替换，用以压缩空间。
  • 最后，如果记录的两个map中，数字出现重叠（可以通过最小值来判断），则意味着该数字在两边都出现过，就将母牛数加一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#Python
class Solution:
    def getHint(self, secret: str, guess: str) -> str:
        mapS, mapG = {}, {}
        a, b = 0, 0
        for i in range(len(secret)):
            if secret[i] == guess[i]:
                a += 1
            else:
                if secret[i] not in mapS:
                    mapS[secret[i]] = 1
                else:
                    mapS[secret[i]] += 1

                if guess[i] not in mapG:
                    mapG[guess[i]] = 1
                else:
                    mapG[guess[i]] += 1

        for key in mapS.keys():
            if key in mapG:
                b += min(mapS[key], mapG[key])

        return str(a)+'A'+str(b)+'B'

执行耗时:44 ms,击败了88.82% 的Python3用户
内存消耗:13.5 MB,击败了16.77% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
    public String getHint(String secret, String guess) {
        int[] mapS = new int[10];
        int[] mapG = new int[10];
        int a = 0, b = 0;
        for(int i = 0; i < secret.length(); i++){
            if(secret.charAt(i) == guess.charAt(i)) a++;
            else{
                mapS[secret.charAt(i) - '0']++;
                mapG[guess.charAt(i) - '0']++;
            }
        }
        for(int i = 0; i < 10; i++){
            b += Math.min(mapS[i], mapG[i]);
        }
        return a + "A" + b + "B"; 
    }
}

执行用时：8 ms, 在所有 Java 提交中击败了34.92% 的用户
内存消耗：38.5 MB, 在所有 Java 提交中击败了41.70% 的用户

11.LRU缓存机制

LRU 是 Least Recently Used 的缩写，译为最近最少使用。它的理论基础为“最近使用的数据会在未来一段时期内仍然被使用，已经很久没有使用的数据大概率在未来很长一段时间仍然不会被使用”由于该思想非常契合业务场景 ，并且可以解决很多实际开发中的问题，所以我们经常通过 LRU 的思想来作缓存，一般也将其称为LRU缓存机制。

第146题：LRU缓存机制
运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作：获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1 。

写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:你是否可以在 O(1) 时间复杂度内完成这两种操作？

示例:

1
2
3
4
5
6
7
8
9
10
LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回  1
cache.put(3, 3);    // 该操作会使得密钥 2 作废
cache.get(2);       // 返回 -1 (未找到)
cache.put(4, 4);    // 该操作会使得密钥 1 作废
cache.get(1);       // 返回 -1 (未找到)
cache.get(3);       // 返回  3
cache.get(4);       // 返回  4

方法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#Python
class LRUCache:

    def __init__(self, capacity: int):
        self.capacity = capacity
        self.cache = {}

    def get(self, key: int) -> int:
        # 搜索不到返回-1
        if key not in self.cache:
            return -1
        # 取出缓存中的key并赋值,使最近被使用的排在最后面
        self.cache[key] = self.cache.pop(key)
        return self.cache[key]

    def put(self, key: int, value: int) -> None:
        # 如存在就先删除key
        if key in self.cache:
            self.cache.pop(key)
        # 先放「密钥/数据值」，之后再判断是否达到上限
        self.cache[key] = value
        #  若超出容量则取最前面的删除，即最近最少使用
        if len(self.cache) > self.capacity:
            x = list(self.cache)[0]
            self.cache.pop(x)

执行耗时:232 ms,击败了54.22% 的Python3用户
内存消耗:21.8 MB,击败了65.84% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Java
class LRUCache {
    
    private LinkedHashMap<Integer, Integer> map = new LinkedHashMap<>();
    private int capacity;

    public LRUCache(int capacity) {
        this.capacity = capacity;
    }
    
    public int get(int key) {
        if(!map.containsKey(key)) return -1;
        int value = map.remove(key);
        map.put(key, value);
        return map.get(key);
    }
    
    public void put(int key, int value) {
        if(map.containsKey(key)) map.remove(key);
        map.put(key, value);
        if(map.size() > capacity) map.remove(map.keySet().iterator().next());
    }
}

执行用时：21 ms, 在所有 Java 提交中击败了45.53% 的用户
内存消耗：46.7 MB, 在所有 Java 提交中击败了29.06% 的用户

方法二：优化

py的原生dict自带链表，已经实现了collections.OrderedDict的绝大部分功能，继承就好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#Python
class LRUCache(dict):

    def __init__(self, capacity: int):
        self.c = capacity

    def get(self, key: int) -> int:
        if key in self:
            self[key] = self.pop(key)
            return self[key]
        return -1

    def put(self, key: int, value: int) -> None:
        key in self and self.pop(key)
        self[key] = value
        len(self) > self.c and self.pop(next(iter(self)))

执行耗时:164 ms,击败了99.39% 的Python3用户
内存消耗:21.8 MB,击败了67.73% 的Python3用户

Java的LinkedHashMap已实现removeEldestEntry()方法用于检查是否删除最旧的条目，只需重写即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//Java
class LRUCache extends LinkedHashMap<Integer, Integer>{
    private int capacity;
    
    public LRUCache(int capacity) {
        // 加载因子，一般是 0.75f
        // true: 是访问的顺序，也就是谁最先访问，就排在第一位  
        // false:存放顺序，就是你put 元素的时候的顺序  
        super(capacity, 0.75F, true);
        this.capacity = capacity;
    }

    public int get(int key) {
        return super.getOrDefault(key, -1);
    }

    public void put(int key, int value) {
        super.put(key, value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity; 
    }
}

执行用时：20 ms, 在所有 Java 提交中击败了56.47% 的用户
内存消耗：46.6 MB, 在所有 Java 提交中击败了46.56% 的用户

12.最小的k个数

剑指offer第40题：最小的k个数
输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：

1
2
输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：

1
2
输入：arr = [0,1,2,1], k = 1
输出：[0]

限制：

1
2
0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000

堆的特性是父节点的值总是比其两个子节点的值大或小。如果父节点比它的两个子节点的值都要大，我们叫做大顶堆。如果父节点比它的两个子节点的值都要小，我们叫做小顶堆。

我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子。


大顶堆，满足以下公式: arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小顶堆也一样：


小顶堆，满足以下公式: arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

上面我们学习了大顶堆，现在考虑如何用大根堆进行求解。

首先，我们创建一个大小为k的大顶堆。假如数组为[4,5,1,6,2,7,3,8]，k=4。大概是下面这样：


我想肯定这里有不知道如何建堆的同学。记住：对于一个没有维护过的堆（完全二叉树），我们可以从其最后一个节点的父节点开始进行调整。这个不需要死记硬背，其实就是一个层层调节的过程。

从最后一个节点的父节点调整


继续向上调整

继续向上调整

然后我们从下标 k 继续开始依次遍历数组的剩余元素。如果元素小于堆顶元素，那么取出堆顶元素，将当前元素入堆。在上面的示例中 ，因为2小于堆顶元素6，所以将2入堆。我们发现现在的完全二叉树不满足大顶堆，所以对其进行调整。
调整前

调整后

继续重复上述步骤，依次将7,3,8入堆。这里因为7和8都大于堆顶元素5，所以只有3会入堆。
调整前

调整后

最后得到的堆，就是我们想要的结果。由于堆的大小是 K，所以这里空间复杂度是O(K)，时间复杂度是O(NlogK)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#Python
class Solution:
    def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
        if k == 0:
            return []
        # 最小的k个数 最大堆
        # 最大堆 顶点最大
        def maxHeapfy(maxHeap, i, n):
            # 左右子节点
            left = 2 * i + 1
            right = 2 * i + 2
            # 假定当前节点最大
            maxPoint = i
            # 和当前节点的左右节点比较，如果节点中有更大的数，那么交换，并继续对交换后的节点进行维护
            if left < n and maxHeap[left] > maxHeap[maxPoint]:
                maxPoint = left
            if right < n and maxHeap[right] > maxHeap[maxPoint]:
                maxPoint = right
            # 如果最大的数不是节点i的话，那么交换后，调整节点i的子树。
            if maxPoint != i:
                maxHeap[i], maxHeap[maxPoint] = maxHeap[maxPoint], maxHeap[i]
                maxHeapfy(maxHeap, maxPoint, n)
        # 初始化 取前k个树，组成最大堆
        maxHeap = arr[:k]
        # 对于一个还没维护过的堆，从他的最后一个节点的父节点开始进行调整。
        for i in range(k // 2 - 1, -1, -1):
            maxHeapfy(maxHeap, i, k)
        # 继续调整后面节点
        for i in range(k, len(arr)):
            # 如果元素小于堆顶元素，那么取出堆顶元素，将当前元素入堆
            if arr[i] < maxHeap[0]:
                maxHeap[0] = arr[i]
                maxHeapfy(maxHeap, 0, k)
        # 最后得到的堆，就是我们想要的结果
        return maxHeap

执行耗时:136 ms,击败了26.01% 的Python3用户
内存消耗:14.5 MB,击败了57.67% 的Python3用户

1
2
3
4
5
6
7
8
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        int[] res = new int[k];
        Arrays.sort(arr);
        System.arraycopy(arr, 0, res, 0, k);
        return res;
    }
}

执行用时：7 ms, 在所有 Java 提交中击败了72.61% 的用户
内存消耗：39.8 MB, 在所有 Java 提交中击败了58.60% 的用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0 || arr.length == 0) return new int[0];
        // 默认是小根堆，实现大根堆需要重写一下比较器。
        Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> v2 - v1);
        for (int num: arr) {
            if (pq.size() < k) {
                pq.offer(num);
            } else if (num < pq.peek()) {
                pq.poll();
                pq.offer(num);
            }
        }
        // 返回堆中的元素
        int[] res = new int[k];
        int idx = 0;
        for(int num: pq) {
            res[idx++] = num;
        }
        return res;
    }
}

执行用时：14 ms, 在所有 Java 提交中击败了41.61% 的用户
内存消耗：39.8 MB, 在所有 Java 提交中击败了57.97% 的用户

13.不同路径

第62题：不同路径
一个机器人位于一个 m x n 网格的左上角，起始点在下图中标记为“Start”。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角，在下图中标记为“Finish”。 问：总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

1
2
3
4
5
6
7
8
输入: m = 3, n = 2
输出: 3

解释:
从左上角开始，总共有 3 条路径可以到达右下角。
\1. 向右 -> 向右 -> 向下
\2. 向右 -> 向下 -> 向右
\3. 向下 -> 向右 -> 向右

示例 2:

1
2
输入: m = 7, n = 3
输出: 28

这道题属于相当标准的动态规划，虽然还有一些公式法等其他解法，但是如果面试官问到，基本就是想考察你的动态规划。

因为有横纵坐标，明显属于二维DP。我们定义DP[i][j]表示到达i行j列的最多路径。同时，因为第0行和第0列都只有一条路径，所以需要初始化为1。

状态转移方程一目了然，dp[i][j] = dp[i-1][j] +dp[i][j-1]

1
2
3
4
5
6
7
8
9
#Python
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        # 初始化为1，因为第0行和第0列为1
        dp = [[ 1 for i in range(n)] for i in range(m)]
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
        return dp[-1][-1]

执行耗时:44 ms,击败了41.96% 的Python3用户
内存消耗:13.7 MB,击败了5.03% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                if(i==0 || j==0) dp[i][j] = 1;
                else dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.6 MB, 在所有 Java 提交中击败了5.30% 的用户

优化

上面的答案，如果在面试时给出，可以给到7分，后面3分怎么拿，我们真的需要用一个二维数组来存储吗？一起看下！

我们使用二维数组记录状态。但是这里观察一下，每一个格子可能的路径，都是由左边的格子和上面的格子的总路径计算而来， 对于之前更早的数据，其实已经用不到了。如计算第三行时，已经用不到第一行的数据了。

那我们只要能定义一个状态，同时可以表示左边的格子和上面的格子，是不是就可以解决问题？所以我们定义状态dp[j]，用来表示当前行到达第j列的最多路径。这个“当前行”三个字很重要，比如我们要计算dp[3]，因为还没有计算出，所以这时dp[3]保存的其实是4（上一行的数据），而dp[2]由于已经计算出了，所以保存的是6（当前行的数据）。理解了这个，就理解如何压缩状态。

1
2
3
4
5
6
7
8
#Python
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [1 for i in range(n)]
        for i in range(1, m):
            for j in range(1, n):
                dp[j] = dp[j] + dp[j-1]
        return dp[-1]

执行耗时:40 ms,击败了67.50% 的Python3用户
内存消耗:13.6 MB,击败了8.16% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int uniquePaths(int m, int n) {
        int[] dp = new int[n];
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                if(i==0 || j==0) dp[j] = 1;
                else dp[j] = dp[j-1] + dp[j];
            }
        }
        return dp[n-1];
    }
}

14.不同路径-障碍物

第63题：不同路径 - 障碍物
一个机器人位于一个 m x n 网格的左上角，起始点在下图中标记为“Start”。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角，在下图中标记为“Finish”。现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？ 问总共有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

说明： m 和 n 的值均不超过 100。

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
输入:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出: 2

解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
\1. 向右 -> 向右 -> 向下 -> 向下
\2. 向下 -> 向下 -> 向右 -> 向右

首先我们还是定义状态，用DP[i][j]表示到达i行j列的最多路径。同时，因为第0行和第0列都只有一条路径，所以需要初始化为1。但有一点不一样的就是：如果在0行0列中遇到障碍物，后面的就都是0，意为此路不通。

完成了初始化，下面就是状态转移方程。和没有障碍物的相比没什么特别的，仍然是dp[i][j] = dp[i-1][j]+dp[i][j-1]。唯一需要处理的是：如果恰好[i][j]位置上有障碍物，则dp[i][j]为0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#Python
class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        if obstacleGrid[0][0] == 1:
            return 0
        dp = [[1 for i in range(len(obstacleGrid[0]))] for i in range(len(obstacleGrid))]

        for j in range(1, len(obstacleGrid[0])):
            dp[0][j] = 0 if obstacleGrid[0][j] == 1 else dp[0][j-1]
        for i in range(1, len(obstacleGrid)):
            dp[i][0] = 0 if obstacleGrid[i][0] == 1 else dp[i-1][0]

        for i in range(1, len(obstacleGrid)):
            for j in range(1, len(obstacleGrid[0])):
                dp[i][j] = 0 if obstacleGrid[i][j] == 1 else dp[i-1][j]+dp[i][j-1]
        return dp[-1][-1]

执行耗时:40 ms,击败了73.20% 的Python3用户
内存消耗:13.7 MB,击败了5.03% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//Java
class Solution {

    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for(int row = 0; row < m; row++){
            for(int col = 0; col < n; col++){
                if(row == 0 && col == 0) dp[row][col] = obstacleGrid[row][col] == 1? 0: 1;
                else if(row == 0) dp[row][col] = obstacleGrid[row][col] == 1? 0: dp[row][col-1];
                else if(col == 0) dp[row][col] = obstacleGrid[row][col] == 1? 0: dp[row-1][col];
                else{
                    dp[row][col] = obstacleGrid[row][col] == 1? 0: dp[row-1][col]+dp[row][col-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：37.7 MB, 在所有 Java 提交中击败了60.14% 的用户

优化

1
2
3
4
5
6
7
8
9
10
11
12
#Python
class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m, n = len(obstacleGrid), len(obstacleGrid[0]),
        dp = [1] + [0] * (n-1)
        for i in range(m):
            for j in range(n):
                if obstacleGrid[i][j]:
                    dp[j] = 0
                elif j > 0:
                    dp[j] = dp[j] + dp[j - 1]
        return dp[-1]

执行耗时:36 ms,击败了89.96% 的Python3用户
内存消耗:13.4 MB,击败了54.45% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//Java
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[] dp = new int[n];
        dp[0] = 1;
        for(int row = 0; row < m; row++){
            for(int col = 0; col < n; col++){
                if(obstacleGrid[row][col] == 1) dp[col] = 0;
                else if(col > 0) dp[col] = dp[col-1] + dp[col];
            }
        }
        return dp[n-1];
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：37.8 MB, 在所有 Java 提交中击败了52.90% 的用户

15.盛最多水的容器

第11题：盛最多水的容器
给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例：

1
2
输入：[1,8,6,2,5,4,8,3,7] 
输出：49

观察可得，垂直的两条线段将会与坐标轴构成一个矩形区域，较短线段的长度将会作为矩形区域的宽度，两线间距将会作为矩形区域的长度，我们求解容纳水的最大值，实为找到该矩形最大化的区域面积。

首先，本题自然可以暴力求解，只要找到每对可能出现的线段组合，然后找出这些情况下的最大面积。这种解法直接略过，大家有兴趣可以下去自己尝试。这道题比较经典是是使用双指针进行求解，已经会的朋友不妨复习复习。

我们初始化两个指针，分别指向两边，构成我们的第一个矩形区域。

根据木桶原理，水的高度取决于短的一侧。我们总是选择将短的一侧向长的一侧移动。并且在每一次的移动中，我们记录下来当前面积大小。

一直到两个棒子撞在一起。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#Python
class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height) - 1
        maxArea = 0
        while left < right:
            if height[left] < height[right]:
                maxArea = max(maxArea, height[left] * (right - left))
                left += 1
            else:
                maxArea = max(maxArea, height[right] * (right - left))
                right -= 1
        return maxArea

执行耗时:64 ms,击败了90.74% 的Python3用户
内存消耗:14.9 MB,击败了38.00% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//Java
class Solution {
    public int maxArea(int[] height) {
        int left = 0, right = height.length - 1;
        int maxArea = 0;
        while(left < right){
            if(height[left] < height[right]){
                maxArea = Math.max(maxArea, height[left]*(right - left));
                left++;
            }
            else{
                maxArea = Math.max(maxArea, height[right]*(right - left));
                right--;
            }
        }
        return maxArea;
    }
}

执行用时：3 ms, 在所有 Java 提交中击败了94.88% 的用户
内存消耗：51.7 MB, 在所有 Java 提交中击败了53.67% 的用户

16.扑克牌中的顺子容器

剑指offer第61题：扑克牌中的顺子
从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的。2～10为数字本身，A为1，J为11，Q为12，K为13，而大、小王为 0 ，可以看成任意数字。A 不能视为 14。

示例 1:

1
2
输入: [1,2,3,4,5]
输出: True

示例 2:

1
2
输入: [0,0,1,2,5]
输出: True

限制：

1
2
数组长度为 5 
数组的数取值为 [0, 13]

数组长度限制了是5，非常省事，意味着我们不需要一些额外的处理。拿到牌，第一个想法排序！因为是5连，无论接没接到大小王，最小值和最大值之间，一定小于5。

排序后，我们通过累积每两张牌之间的差值，来计算最小值和最大值中间的总差值。

拿到了王，就相当于拿到了通行证，直接跳过。因为是排序的牌，如果接到对子，也就意味着不是五连，直接返回false。

1
2
3
4
5
6
7
8
9
10
11
12
#Python
class Solution:
    def isStraight(self, nums: List[int]) -> bool:
        nums.sort()
        sub = 0
        for i in range(len(nums)-1):
            if nums[i] == 0:
                continue
            if nums[i] == nums[i+1]:
                return False
            sub += nums[i+1] - nums[i]
        return sub < 5

执行耗时:44 ms,击败了40.35% 的Python3用户
内存消耗:13.5 MB,击败了16.56% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public boolean isStraight(int[] nums) {
        Arrays.sort(nums);
        int sub = 0;
        for(int i = 0; i < nums.length - 1; i++){
            if(nums[i] == 0) continue;
            if(nums[i] == nums[i+1]) return false;
            sub += (nums[i+1] - nums[i]);
        }
        return sub < 5; 
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了91.62% 的用户
内存消耗：35.7 MB, 在所有 Java 提交中击败了86.90% 的用户

17.整数拆分

第343题：整数拆分
给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。返回你可以获得的最大乘积。

示例 1:

1
2
3
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

1
2
3
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

说明: 你可以假设 n 不小于 2 且不大于 58。

要对一个整数进行拆分，并且要使这些拆分完后的因子的乘积最大。我们可以先尝试拆分几个数值，测试一下。

通过观察，首先肯定可以明确，2 和 3 是没办法进行拆分的最小因子。同时，我们好像能看出来：

  • 只要把 n 尽可能的拆分成包含3的组合，就可以得到最大值。
  • 如果没办法拆成 3 的组合，就退一步拆成 2 的组合。
  • 对于 3 和 2 ，没办法再进行拆分。

根据分析，我们尝试使用贪心进行求解。因为一个数（假设为n）除以另一个数，总是包括整数部分（x）和余数部分（y）。那刚才也得到了，最优因子是3，所以我们需要让 n/3，这样的话，余数可能是 1,2 两种可能性。

  • 如果余数是 1 ，刚才我们也分析过，对于 1 的拆分是没有意义的，所以我们退一步，将最后一次的 3 和 1 的拆分，用 2 和 2 代替。
  • 如果余数是 2 ，那不消多说，直接乘以最后的 2 即可。

方法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#Python
class Solution:
    def integerBreak(self, n: int) -> int:
        if n <= 3:
            return n - 1
        # 恰好整除，直接为3^x
        if n % 3 == 0:
            return 3 ** (n // 3)
        # 余数为1，退一步 3^(x-1)*2*2
        elif n % 3 == 1:
            return 3 ** (n // 3 - 1) * 4
        # 余数为2，直接乘以2
        else:
            return 3 ** (n // 3) * 2

执行耗时:32 ms,击败了96.37% 的Python3用户
内存消耗:13.5 MB,击败了31.43% 的Python3用户

1
2
3
4
5
6
7
8
9
//Java
class Solution {
    public int integerBreak(int n) {
        if(n <= 3) return n-1;
        if(n % 3 == 0) return (int)Math.pow(3, n/3);
        else if(n % 3 == 1) return (int)Math.pow(3, n/3-1)*4;
        else return (int)Math.pow(3, n/3)*2;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.3 MB, 在所有 Java 提交中击败了31.03% 的用户

方法二：动态规划

dp[i]代表 i 拆分之后得到的乘积的最大的元素，比如dp[4]就保存将4拆分后得到的最大的乘积。状态转移方程式为 dp[i]=max(dp[i], (i-j)*max(dp[j],j))

整体思路就是这样，将一个大的问题，分解成一个一个的小问题，然后完成一个自底向上的过程。举一个例子，比如计算 10 ，可以拆分 6 和 4 ，因为 6 的最大值 3x3，以及 4 的最大值 2x2 都已经得到，所以就替换成 9 和 4 ，也就是 10=3x3x4。

1
2
3
4
5
6
7
8
9
#Python
class Solution:
    def integerBreak(self, n: int) -> int:
        dp = [0] * (n + 1)
        dp[1] = 1
        for i in range(2, n + 1):
            for j in range(i):
                dp[i] = max(dp[i], max(dp[j], j) * (i - j))
        return dp[n]

执行耗时:44 ms,击败了57.61% 的Python3用户
内存消耗:13.5 MB,击败了31.43% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n+1];
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            for(int j = 0; j < i; j++){
                dp[i] = Math.max(dp[i], Math.max(dp[j], j)*(i - j));
            }
        }
        return dp[n];
    }
}

执行用时：2 ms, 在所有 Java 提交中击败了12.89% 的用户
内存消耗：35.1 MB, 在所有 Java 提交中击败了80.09% 的用户

18.移动石子直到连续

第1033题：移动石子直到连续
三枚石子放置在数轴上，位置分别为 a，b，c。每一回合，我们假设这三枚石子当前分别位于位置 x, y, z 且 x < y < z。从位置 x 或者是位置 z 拿起一枚石子，并将该石子移动到某一整数位置 k 处，其中 x < k < z 且 k != y。当你无法进行任何移动时，即，这些石子的位置连续时，游戏结束。要使游戏结束，你可以执行的最小和最大移动次数分别是多少？以长度为 2 的数组形式返回答案：answer = [minimum_moves, maximum_moves]

示例1：

1
2
3
输入：a = 1, b = 2, c = 5
输出：[1, 2]
解释：将石子从 5 移动到 4 再移动到 3，或者我们可以直接将石子移动到 3。

示例 2：

1
2
3
输入：a = 4, b = 3, c = 2
输出：[0, 0]
解释：我们无法进行任何移动。

提示：

1
2
3
4
1 <= a <= 100
1 <= b <= 100
1 <= c <= 100
a != b, b != c, c != a

读懂了题意，开始进行分析。首先可以明确，每一次我们其实是从边上来挑选石子，然后往中间进行移动。所以，我们首先得找到min（左），max（右）以及mid（中）三个值。我们设，min和mid中的距离为x，max和min中的距离为y。大概就是下面这样：

然后只需要计算x和y的和，就是我们要找的最大值。而最小值，就很容易了，只有0,1,2三种可能性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Python
class Solution:
    def numMovesStones(self, a: int, b: int, c: int) -> List[int]:
    	# 将石子从小到大排序
        arr = sorted([a, b, c])
        x = arr[1] - arr[0] - 1
        y = arr[2] - arr[1] - 1
        max = x + y
        min = 0
        if x != 0 or y != 0:
            if x > 1 and y > 1:
                min = 2
            else:
                min = 1
        return [min, max]

执行耗时:28 ms,击败了99.36% 的Python3用户
内存消耗:13.5 MB,击败了33.33% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//Java
class Solution {
    public int[] numMovesStones(int a, int b, int c) {
        int[] arr = new int[]{a, b ,c};
        Arrays.sort(arr);
        int x = arr[1] - arr[0] -1;
        int y = arr[2] - arr[1] -1;
        int max_move = x + y;
        int min_move = 0;
        if(x != 0 || y != 0){
            if(x > 1 && y > 1) min_move = 2;
            else min_move = 1;
        }
        return new int[]{min_move, max_move};
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了49.13% 的用户
内存消耗：36.1 MB, 在所有 Java 提交中击败了93.93% 的用户

19.Nim游戏

第292题：Nim 游戏
你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头，每次你们轮流拿掉 1 - 3 块石头。拿掉最后一块石头的人就是获胜者。你作为先手。 你们是聪明人，每一步都是最优解。编写一个函数，来判断你是否可以在给定石头数量的情况下赢得游戏。

示例:

1
2
3
4
输入: 4
输出: false 
解释: 如果堆中有 4 块石头，那么你永远不会赢得比赛；
     因为无论你拿走 1 块、2 块 还是 3 块石头，最后一块石头总是会被你的朋友拿走。

首先如果石头数小于4个，那么因为你是先手，一把拿走，肯定会赢。

而如果石头是4个，那不管你是拿了1,2,3个，最后一个都可以被你的对手拿走，所以怎么样都赢不了。

再继续分析到8个石头：对于5,6,7而言，你只需要对应的拿走1,2,3，然后留下4个，则对方必输。但是如果你要面对的是8，不管先拿（1,2,3）个，另一个人都可以通过 8-(1,2,3) ，使得你面对4个石头，则你必输无疑。通过观察，我们发现，好像是只要N是4的倍数，我们就必输无疑。

1
2
3
4
#Python
class Solution:
    def canWinNim(self, n: int) -> bool:
        return n % 4 != 0

执行耗时:40 ms,击败了55.90% 的Python3用户
内存消耗:13.5 MB,击败了11.08% 的Python3用户

1
2
3
4
5
6
//Java
class Solution {
    public boolean canWinNim(int n) {
        return n % 4 != 0;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：35.4 MB, 在所有 Java 提交中击败了16.27% 的用户

20.寻找两个正序数组的中位数

第4题：寻找两个正序数组的中位数
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。你可以假设 nums1 和 nums2 不会同时为空。

示例 1:

1
2
3
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0

示例 2:

1
2
3
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5

示例 3：

1
2
输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

示例 4：

1
2
输入：nums1 = [], nums2 = [1]
输出：1.00000

示例 5：

1
2
输入：nums1 = [2], nums2 = []
输出：2.00000

一般如果题目要求时间复杂度在O(log(n))，大部分都是可以使用二分的思想来进行求解。

如果只有一个有序数组，我们需要找中位数，那肯定需要判断元素是奇数个还是偶数个，如果是奇数个那最中间的就是中位数，如果是偶数个的话，那就是最中间两个数的和除以2。

那如果是两个数组，也是一样的，我们先求出两个数组长度之和。如果为奇数，就找中间的那个数，也就是 (长度之和 + 1)/2 。如果为偶数，那就找 长度之和/2。比如下面的 (9 + 5)/2 = 7，那我们最终就是找到排列第7位的值。

现在的问题是，我们如何用二分的思想来找到中间排列第7位的数。这里有一种不太好想到的方式，是用删的方式，因为如果我们可以把多余的数排除掉，最终剩下的那个数，是不是就是我们要找的数？ 对于上面的数组，我们可以先删掉 7/2=3 个数。那这里，可以选择删上面的，也可以选择删下面的。那这里因为 i<j，所以我们选择删除上面的3个数。

（删除前）

（删除后）

由于我们已经排除掉了 3 个数字，现在对于两个数组，我们需要找到7-3=4的数字，来进行下一步运算。我们可以继续删掉4/2=2个数。我们比较i和j的值，删除小的一边。

（删除前）

（删除后）

继续上面的步骤，我们删除 2/2=1 个数。同理，比较7和6的大小，删除小的一边。删完后是下面这样：

（7和6，删除6）

不要忘记我们的目的，我们是为了找第7小的数。此时，两个数组的第一个元素，哪个小，就是我们要找的那个数。因为7<8，所以7就是我们要找的第7小的数。

这里有一点比较特殊的，如果在删除过程中，我们要删除的K/2个数，大于其中一边的数组长度，那我们就将小的一侧数组元素都删除。比如下面这个，此时7/2=3，但是下面的数组只有2个元素，我们就将它全部删除。

删完之后，此时因为只删除了2个元素，所以k变成了5。那我们只需要返回其中一边的第5个元素就ok。

整个上面的过程，完成了本题的算法架构！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#Python
class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        def findK(nums1, i, nums2, j, k):
            # 特殊情况：要删除的个数大于其中一边的数组长度
            if i >= len1:
                return nums2[j + k - 1]
            # 特殊情况：要删除的个数大于其中一边的数组长度
            if j >= len2:
                return nums1[i + k - 1]
            # 正常情况
            if k == 1:
                return min(nums1[i], nums2[j])
            # 计算出每次要比较的两个数的值，来决定"删除"哪边的元素
            mid1 = nums1[i + k // 2 - 1] if (i + k // 2 - 1) < len1 else inf
            mid2 = nums2[j + k // 2 - 1] if (j + k // 2 - 1) < len2 else inf
            #　通过递归的方式，来模拟删除掉前K//2个元素
            if mid1 < mid2:
                return findK(nums1, i + k // 2, nums2, j, k - k // 2)
            return findK(nums1, i, nums2, j + k // 2, k - k // 2)

        len1 = len(nums1)
        len2 = len(nums2)
        total = len1 + len2
        # 比如总数为偶数14，就要找第7个和第8个
        # 比如总数为奇数5，就要找第3个
        left = (total + 1) // 2
        right = (total + 2) // 2
        return (findK(nums1, 0, nums2, 0, left) + findK(nums1, 0, nums2, 0, right)) / 2

执行耗时:52 ms,击败了77.16% 的Python3用户
内存消耗:13.8 MB,击败了5.17% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//Java
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length, length2 = nums2.length;
        int totalLength = length1 + length2;
        int left = (totalLength + 1) / 2, right = (totalLength + 2) / 2;
        double median = (getKthElement(nums1, nums2, left) + getKthElement(nums1, nums2, right)) / 2.0;
        return median;
    }

    public int getKthElement(int[] nums1, int[] nums2, int k) {
         /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
         * 这里的 "/" 表示整除
         * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
         * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
         * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
         * 这样 pivot 本身最大也只能是第 k-1 小的元素
         * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
         * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
         * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
         */

        int length1 = nums1.length, length2 = nums2.length;
        int index1 = 0, index2 = 0;
        int kthElement = 0;

        while (true) {
            // 边界情况
            if (index1 == length1) {
                return nums2[index2 + k - 1];
            }
            if (index2 == length2) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return Math.min(nums1[index1], nums2[index2]);
            }
            
            // 正常情况
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, length1) - 1;
            int newIndex2 = Math.min(index2 + half, length2) - 1;
            int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k -= (newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            } else {
                k -= (newIndex2 - index2 + 1);
                index2 = newIndex2 + 1;
            }
        }
    }
}

执行用时：3 ms, 在所有 Java 提交中击败了82.06% 的用户
内存消耗：39.2 MB, 在所有 Java 提交中击败了99.34% 的用户

21.第k个最大元素

第215题：第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

1
2
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

1
2
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

这种题目，从个人来讲，我一般是比较偏好使用堆来做的。毕竟大小顶堆，刚好有着与本类题型契合的特性。我们对其构造一个小顶堆（每个结点的值均不大于其左右孩子结点的值，堆顶元素为整个堆的最小值），整个过程是这样：

构造一个小顶堆，依次将元素放入堆中，并保证堆中元素为k。

如果当前元素小于堆顶元素，那基本就不用看了（因为我们要找的是 排序后的第 k 个最大的元素）

自然，如果我们遇到比堆顶元素大的元素，就把它放入到堆中。

重复上面的步骤。

方法一：小顶堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#Python
class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        # 最大的k个数 最小堆
        # 最小堆 顶点最小
        def minHeapfy(minHeap, i, k):
            # 左右子节点
            left = 2 * i + 1
            right = 2 * i + 2
            # 假定当前节点最小
            minPoint = i
            # 和当前节点的左右节点比较，如果节点中有更小的数，那么交换，并继续对交换后的节点进行维护
            if left < k and minHeap[left] < minHeap[minPoint]:
                minPoint = left
            if right < k and minHeap[right] < minHeap[minPoint]:
                minPoint = right
            # 如果最小的数不是节点i的话，那么交换后，调整节点i的子树。
            if minPoint != i:
                minHeap[i], minHeap[minPoint] = minHeap[minPoint], minHeap[i]
                minHeapfy(minHeap, minPoint, k)
        # 初始化 取前k个树，组成最小堆
        minHeap = nums[:k]
        # 对于一个还没维护过的堆，从他的最后一个节点的父节点开始进行调整。
        for i in range(k // 2 - 1, -1, -1):
            minHeapfy(minHeap, i, k)
        # 继续调整后面节点
        for i in range(k, len(nums)):
            # 如果元素大于堆顶元素，那么取出堆顶元素，将当前元素入堆
            if nums[i] > minHeap[0]:
                minHeap[0] = nums[i]
                minHeapfy(minHeap, 0, k)
        # 最后得到的堆顶，就是我们想要的结果
        return minHeap[0]

执行耗时:64 ms,击败了44.82% 的Python3用户
内存消耗:15.3 MB,击败了14.45% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//Java
class Solution {
    public int findKthLargest(int[] nums, int k) {
        int[] minHeap = Arrays.copyOf(nums, k);
        for(int i = k / 2 - 1; i > -1; i--) minHeap(minHeap, i, k);
        for(int i = k; i < nums.length; i++){
            if(nums[i] > minHeap[0]){
                minHeap[0] = nums[i];
                minHeap(minHeap, 0, k);
            }
        }
        return minHeap[0];

    }

    public void minHeap(int[] nums, int i, int k){
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int minPoint = i;
        if(left < k && nums[left] < nums[minPoint]) minPoint = left;
        if(right < k && nums[right] < nums[minPoint]) minPoint = right;
        if(minPoint != i){
            int tmp = nums[i];
            nums[i] = nums[minPoint];
            nums[minPoint] = tmp;
            minHeap(nums, minPoint, k);
        }
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了99.35% 的用户
内存消耗：38.8 MB, 在所有 Java 提交中击败了51.50% 的用户

方法二：调用内置函数

python可以使用heapq.nlargest 或 heapq.nsmallest，来找出某个集合中找出最大或最小的N个元素。

1
2
3
4
#Python
class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        return heapq.nlargest(k, nums)[-1]  # [6,5]

执行耗时:40 ms,击败了91.38% 的Python3用户
内存消耗:15.3 MB,击败了14.45% 的Python3用户

第347题：前 K 个高频元素
给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

1
2
输入: [1,1,1,2,2,3] 和 k = 2
输出: [1, 2]

示例 2:

1
2
输入: [1] 和 k = 1
输出: [1]

这题也是同样的道理，只是需要先统计各元素出现的次数，然后按照次数的大小为基准加入小顶堆，这里提供Java内置小顶堆函数的用法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int num: nums) map.put(num, map.getOrDefault(num, 0) + 1);
        Queue<Integer> minHeap = new PriorityQueue<>((v1, v2) -> map.get(v1) - map.get(v2));    
        map.forEach((num, cnt) -> {
            if (minHeap.size() < k) {
                minHeap.offer(num);
            } else if (map.get(minHeap.peek()) < cnt) {
                minHeap.poll();
                minHeap.offer(num);
            }
        });
        int[] res = new int[k];
        for (int i = 0; i < k; i++) res[i] = minHeap.poll();
        return res;
    }
}

执行用时：18 ms, 在所有 Java 提交中击败了26.53% 的用户
内存消耗：41 MB, 在所有 Java 提交中击败了70.04% 的用户

22.镜面反射

第858题：镜面反射
有一个特殊的正方形房间，每面墙上都有一面镜子。除西南角以外，每个角落都放有一个接受器，编号为 0，1，以及 2。正方形房间的墙壁长度为 p，一束激光从西南角射出，首先会与东墙相遇，入射点到接收器 0 的距离为 q 。返回光线最先遇到的接收器的编号（保证光线最终会遇到一个接收器）。

示例：

1
2
3
输入： p = 2, q = 1
输出： 2
解释： 这条光线在第一次被反射回左边的墙时就遇到了接收器 2

上面的题目绕得很，大概就是这么个意思：

我们知道光是由西南角发出的，也就是左下角。发出之后可能会出现多种情况（注意，下图略过了部分光线反射的情况）。看起来是十分复杂，无迹可寻。

但是如果我们把光线的运动轨迹拆开来看，就可以观测到，光线每经过一次折反，都会在纵向距离上移动 q（首次与东墙相距的距离）。同时，一旦其向上行走的距离为 p 的整数倍，就一定会碰到某个接收点（注意：这里我们不需要考虑北面墙是否存在，根据光的反射定律可得）可以参考一下下面这张图：

问题变得简单了，光线最终向上走的距离，其实就是 p 和 q 的最小公倍数。我们设最小公倍数为 L，会发现如果 L 是 p 的奇数倍，光线则到达北墙（可以参考上面的图）当 L 是 p 的 偶数倍，光线将会射到南墙。

问题来了，如果光线是射向南墙，因为只有一个接收器了，必定只能遇到接收器 0。但是如果射到了北墙，如何区分是 1 和 2。这回到了一个初中数学题，我们可以通过光线与东西墙的接触次数，来判断最终的落点是 1 还是 2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#Python
class Solution:
    def mirrorReflection(self, p: int, q: int) -> int:
        m, n = p, q
        # 最大公约数
        # 假设x和y的最大公约数是m,最小公倍数是n,则xy=mn
        while n > 0:
            r = m % n
            m = n
            n = r
        # 假设x和y的最大公约数是m,最小公倍数是n,则xy=mn
        # 所以最小公倍数为pq/m
        # 若q/m为偶数则最小公倍数为p的偶数倍，射向南墙
        if (q / m) % 2 == 0:
            return 0
        # 否则为奇数倍，判断与东西墙的接触次数
        # 若p/m为偶数则最小公倍数为q的偶数倍，落点为2
        elif (p / m) % 2 == 0:
            return 2
        # 否则落点为1
        else:
            return 1

执行耗时:36 ms,击败了83.16% 的Python3用户
内存消耗:14.9 MB,击败了5.43% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//Java
class Solution {
    public int mirrorReflection(int p, int q) {
        int m = p, n = q;
        while(n > 0){
            int r = m % n;
            m = n;
            n = r;
        }
        if (q / m % 2 == 0) return 0;
        else if(p / m % 2 == 0)  return 2;
        else return 1;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：34.9 MB, 在所有 Java 提交中击败了92.59% 的用户

23.整数转罗马数字

第12题：整数转罗马数字
罗马数字包含以下七种字符：I， V， X，L，C，D 和 M。
1
2
3
4
5
6
7
8
字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。27 写做 XXVII， 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。

X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。

C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个整数，将其转为罗马数字。输入确保在 1 到 3999 的范围内。

示例 1:

1
2
输入: 3
输出: "III"

示例 2:

1
2
输入: 4
输出: "IV"

示例 3:

1
2
输入: 9
输出: "IX"

示例 4:

1
2
3
输入: 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.

示例 5:

1
2
3
输入: 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.

我们把题目中所有的字符列出来，一些特殊的规则也得列出来。假设我们要找的数为2834，大概的流程如下（其实是一种类似贪心的思想）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#Python
class Solution:
    def intToRoman(self, num: int) -> str:
        nums = [1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1]
        romas = ["M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"]
        result = ''
        index = 0
        while num > 0:
            if num >= nums[index]:
                result += romas[index]
                num -= nums[index]
            else:
                index += 1
        return result

执行耗时:52 ms,击败了88.55% 的Python3用户
内存消耗:14.8 MB,击败了5.03% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
    int[] values = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
    String[] symbols = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};

    public String intToRoman(int num) {
        StringBuffer roman = new StringBuffer();
        for (int i = 0; i < values.length; ++i) {
            int value = values[i];
            String symbol = symbols[i];
            while (num >= value) {
                num -= value;
                roman.append(symbol);
            }
            if (num == 0) break;
        }
        return roman.toString();
    }
}

执行用时：6 ms, 在所有 Java 提交中击败了47.30% 的用户
内存消耗：37.8 MB, 在所有 Java 提交中击败了72.05% 的用户

24.荷兰国旗问题

第75题：荷兰国旗问题：现在有若干个红、白、蓝三种颜色的球随机排列成一条直线。现在我们的任务是把这些球按照红、白、蓝排序。
这个问题之所以叫荷兰国旗，是因为我们可以将红白蓝三色小球想象成条状物，有序排列后正好组成荷兰国旗。

大概就是这么个意思：

改成这样：


那总共就三个颜色，我们要区分开来，是不是最少需要两条分隔线？A线的左侧为0，右侧为1。B线的左侧为1，右侧为2。

剩下的是不是只需要把 A线 和 B线 间的数据维护成满足 AB 线的规则就可以了？那要维护 AB 线间的数据，是不是至少你得遍历下 AB 线间的数据？我们从 C 位置处开始。

  • 1）若遍历到的位置为0，则说明它一定位于A的左侧。于是就和A处的元素交换，同时向右移动A和C。
  • 2）若遍历到的位置为1，则说明它一定位于AB之间，满足规则，不需要动弹。只需向右移动C。
  • 3）若遍历到的位置为2，则说明它一定位于B的右侧。于是就和B处的元素交换，交换后只把B向左移动，C仍然指向原位置。（因为交换后的C可能是属于A之前的，所以C仍然指向原位置）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#Python
class Solution:
    def sortColors(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        a = c = 0
        b = len(nums) - 1
        while c <= b:
            if nums[c] == 0:
                nums[a], nums[c] = nums[c], nums[a]
                a += 1
                c += 1
            elif nums[c] == 2:
                nums[c], nums[b] = nums[b], nums[c]
                b -= 1
            else:
                c += 1

执行耗时:36 ms,击败了86.24% 的Python3用户
内存消耗:14.9 MB,击败了5.10% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
class Solution {
    public void sortColors(int[] nums) {
        int l = -1;
        int r = nums.length;
        int cur = 0;
        while(cur < r){
            if(nums[cur] < 1) swap(nums, ++l, cur++);
            else if(nums[cur] > 1) swap(nums, --r, cur);
            else cur++;
        }
    }

    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.8 MB, 在所有 Java 提交中击败了84.85% 的用户

25.六九问题

第1323题：6 和 9 组成的最大数字
给你一个仅由数字 6 和 9 组成的正整数 num。

大概就是这么个意思：

1
2
3
4
5
6
7
8
9
输入：num = 9669
输出：9969

解释：
改变第一位数字可以得到 6669 。
改变第二位数字可以得到 9969 。
改变第三位数字可以得到 9699 。
改变第四位数字可以得到 9666 。
其中最大的数字是 9969 。

我们只要找到 num 中最高位的 6，将其翻转成 9，就可以找到答案。

1
2
3
4
#Python
class Solution:
    def maximum69Number (self, num: int) -> int:
        return int(str(num).replace('6', '9', 1))

执行耗时:60 ms,击败了5.65% 的Python3用户
内存消耗:14.7 MB,击败了5.20% 的Python3用户

1
2
3
4
5
6
7
//Java
class Solution {
    public int maximum69Number (int num) {
        String res = Integer.toString(num);
        return Integer.parseInt(res.replaceFirst("6", "9"));
    }
}

执行用时：5 ms, 在所有 Java 提交中击败了37.53% 的用户
内存消耗：35.3 MB, 在所有 Java 提交中击败了64.39% 的用户

26.有效的数独

第36题：有效的数独
判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。
  • 数字 1-9 在每一行只能出现一次。
  • 数字 1-9 在每一列只能出现一次。
  • 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
输入：
[

  ["5","3",".",".","7",".",".",".","."],

  ["6",".",".","1","9","5",".",".","."],

  [".","9","8",".",".",".",".","6","."],

  ["8",".",".",".","6",".",".",".","3"],

  ["4",".",".","8",".","3",".",".","1"],

  ["7",".",".",".","2",".",".",".","6"],

  [".","6",".",".",".",".","2","8","."],

  [".",".",".","4","1","9",".",".","5"],

  [".",".",".",".","8",".",".","7","9"]

]

输出: true

解释:

数独部分空格内已填入了数字，空白格用 '.' 表示。

说明:

一个有效的数独（部分已被填充）不一定是可解的。

只需要根据以上规则，验证已经填入的数字是否有效即可。

给定数独序列只包含数字 1-9 和字符 ‘.’ 。

给定数独永远是 9x9 形式的。

画出来就是下面这样：

我们要做的就是用程序来完成这个验证的过程，如何验证？那其实就两步：

  • 第一步：遍历数独中的每一个元素
  • 第二步：验证该元素是否满足上述条件

遍历这个没什么好说的，从左到右，从上到下进行遍历即可。就一个两层循环。因为题目本身就是常数级的规模，所以时间复杂度就是 O(1)。

问题来了：如何验证元素在 行 / 列 / 子数独中没有重复项？

其实很简单，我们建立三个数组分别记录每行，每列，每个子数独（子数独就是上面各种颜色的小框框）中出现的数字。

1
2
3
4
//JAVA
int[][] rows = new int[9][9];
int[][] col = new int[9][9];
int[][] sbox = new int[9][9];

当然，刚开始的时候他们都是空的。然后每遍历到一个元素，我们就看看这个元素在里边存不存在，不存在就放进去，存在那说明数独不合法。

比如这个数独。第6行5列为2，那我们就对 rows 和 col 进行设置：（1表示元素存在)
rows[当前行-1][当前元素值-1] = rows[6-1][2-1] = 1
col[当前列-1][当前元素值-1] = col[5-1][2-1] = 1

现在的题是，对于 sbox 该如何设置呢？我们用下面的公式来计算得到：

1
boxIndex = (row / 3) * 3 + columns / 3

其实很容易理解：我们把上面的第6行5列代入到这个公式里，(5 / 3) * 3 + 4 / 3 = 3 + 1 = 4。这个 4 也就代表最终落到 4 的这个小区域中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#Python
class Solution:
    def isValidSudoku(self, board: List[List[str]]) -> bool:
        rows = [[0 for i in range(9)] for i in range(9)]
        cols = [[0 for i in range(9)] for i in range(9)]
        sbox = [[0 for i in range(9)] for i in range(9)]
        for i in range(len(board)):
            for j in range(len(board[0])):
                if board[i][j] != '.':
                    num = int(board[i][j]) - 1
                    boxIndex = (i // 3) * 3 + j // 3
                    if rows[i][num] == 1:
                        return False
                    rows[i][num] = 1

                    if cols[j][num] == 1:
                        return False
                    cols[j][num] = 1

                    if sbox[boxIndex][num] == 1:
                        return False
                    sbox[boxIndex][num] = 1
        return True

执行耗时:56 ms,击败了46.19% 的Python3用户
内存消耗:14.9 MB,击败了5.10% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Java
class Solution {
    public boolean isValidSudoku(char[][] board) {
        int[][] rows = new int[9][9];
        int[][] col = new int[9][9];
        int[][] sbox = new int[9][9];
        for(int i = 0; i < 9; i++){
            for(int j = 0; j < 9; j++){
                if(board[i][j] != '.'){
                    int num = board[i][j] - '0' - 1;
                    int boxIndex = i / 3 * 3 + j / 3;
                    if(rows[i][num] == 1) return false;
                    rows[i][num] = 1;
                    if(col[j][num] == 1) return false;
                    col[j][num] = 1;
                    if(sbox[boxIndex][num] == 1) return false;
                    sbox[boxIndex][num] = 1;
                }
            }
        }
        return true;
    }
}

执行用时：2 ms, 在所有 Java 提交中击败了94.35% 的用户
内存消耗：38.5 MB, 在所有 Java 提交中击败了55.46% 的用户

27.费米估算

问题：北京有多少加油站？
对的，你没看错，这就是原题。。。

截止到2019年，北京共有1063个加油站

这道题目主要考察人的估算能力。而估算界，有一个估算大牛叫做费米。

费米估算，其实说白了就是将正确答案，转化为一系列估算变量的乘法。首先要把变量选的准确，其次要把变量估的准确。回到本题，我们要分析的问题是：北京有多少加油站？

那我们至少得有多少辆车吧？但是并不是所有的车，每天都会上路。所以准确的说我们需要知道每天上路的车有多少。

但是是所有上路的车都需要加油吗？当然不是，所以我们还得改改：每天上路需要加油的车有多少？

知道了每天上路需要加油的车辆数，我们得知道每个加油站可以满足多少辆车吧？

那加油站用什么满足车？自然是油咯。

问题来了，那我们如何知道每天上路需要加油的车辆数？是不是我们可以转化为 北京车辆总数 / 加油频次。

这个加油频次，相信大家就很容易估算出来了。跑滴滴的一天一次油，正常开的话一周一次，开的少一点的话差不多半个月一次。

① 每天上路需要加油的车辆数 ② 每个加油站的容量

所以我们只要回答出上面两个参数，再给出计算公式。就可以很完美的解答本题了！

28.分发饼干

题目455：分发饼干
假设你是一位很棒（多棒？？？）的家长，想要给你的孩子们一些小饼干（不能给大饼干吗？？？）但是，每个孩子最多只能给一块饼干（有毒吧。。。）

对每个孩子 i ，都有一个胃口值 gi ，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j ，都有一个尺寸 sj 。如果 sj >= gi ，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

注意：你可以假设胃口值为正（特么不正难道往外吐吗？？？）。一个小朋友最多只能拥有一块饼干。

示例 :

1
2
3
4
5
6
7
输入: [1,2,3], [1,1] 
输出: 1 

解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

其实策略就很简单了：我们只需要在满足孩子胃口的前提下，尽可能分配小的饼干给到他。

具体怎么做呢，我们把饼干和小朋友都按照从大到小排列。

  • 如果最大的饼干可以满足肚子最大的孩子，那就给他吃，同时比较下一个。
  • 如果最大的饼干不能满足肚子最大的孩子，那就让他饿着，然后看看能不能满足第二个孩子。（有点黑暗系，放弃小朋友）

但是这里有个问题。凭什么就要先满足肚子最大的孩子。按道理讲，肚子越大应该越扛饿才对吧。所以我们换种思路，从肚子最小的孩子开始。

  • 如果最小的饼干可以满足肚子最小的孩子，那就给他吃，同时比较下一个。
  • 如果最小的饼干不能满足肚子最小的孩子，那就扔掉饼干，看看下一个饼干能不能给他吃。（放弃的是饼干）

那这两种其实都算是贪心：

  • 一种是胃口太大轮到下一个孩子
  • 一种是饼干太小轮到下一个饼干

因为要同时控制饼干和小孩，所以我们采用双指针。这里给出先满足小肚子孩子的代码：

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort()
        s.sort()
        gi, si = 0, 0
        while gi < len(g) and si < len(s):
            if g[gi] <= s[si]:
                gi+=1
            si+=1
        return gi

执行耗时:60 ms,击败了92.10% 的Python3用户
内存消耗:16.1 MB,击败了5.14% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
//Java
class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int ch = 0, bis = 0;
        while(ch < g.length && bis < s.length){
            if(g[ch] <= s[bis]) ch++;
            bis++;
        }
        return ch;
    }
}

执行用时：9 ms, 在所有 Java 提交中击败了21.24% 的用户
内存消耗：39.2 MB, 在所有 Java 提交中击败了50.44% 的用户

29.生命游戏

第289题：生命游戏
给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态：1 即为活细胞（live），或 0 即为死细胞（dead）。

每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

  • 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
  • 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
  • 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
  • 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

根据当前状态，写一个函数来计算面板上所有细胞的下一个（一次更新后的）状态。下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。

题目有点复杂，举例说明：

注意：面板上所有格子需要同时被更新：你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子。

最自然的想法是：一个个的更新细胞状态。

已更新细胞的状态会影响到周围其他还未更新细胞状态的计算。这明显不是我们想要的！

那我们最简单的思路：是不是只要我们能一直获取原始数组的数据，不就可以保证更新一直正确了吗！至于在哪里，其实不管是copy一个数组，还是说用hashmap存一下数值其实都ok。

方法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#Python
class Solution:
    def gameOfLife(self, board: List[List[int]]) -> None:
        # 每个细胞统周围八个相邻位置的偏移量
        neighbors = [0, 1, -1]
        # 创建复制数组 copyBoard
        # 注意直接用切片的方式或者list()方式是浅复制，被坑了好久。。。
        copyBoard = [[0] * len(board[0]) for _ in range(len(board))]
        for i in range(len(board)):
            for j in range(len(board[0])):
                copyBoard[i][j] = board[i][j]
        # 遍历面板每一个格子里的细胞
        for row in range(len(board)):
            for col in range(len(board[0])):
                # 对于每一个细胞统计其八个相邻位置里的活细胞数量
                liveNeighbors = 0
                for i in range(3):
                    for j in range(3):
                        if neighbors[i] != 0 or neighbors[j] != 0:
                            r = row + neighbors[i]
                            c = col + neighbors[j]
                            # 查看相邻的细胞是否是活细胞
                            if r < len(board) and r >= 0 and c < len(board[0]) and c >= 0 and copyBoard[r][c] == 1:
                                liveNeighbors += 1
                # 规则 1 或规则 3
                if copyBoard[row][col] == 1 and (liveNeighbors < 2 or liveNeighbors > 3):
                    board[row][col] = 0
                # 规则 4
                if copyBoard[row][col] == 0 and liveNeighbors == 3:
                    board[row][col] = 1

执行耗时:40 ms,击败了71.15% 的Python3用户
内存消耗:14.8 MB,击败了7.69% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//Java
class Solution {
    private int[] neighbors = new int[]{0, 1, -1};
    public void gameOfLife(int[][] board) {
        int[][] copyBoard = new int[board.length][board[0].length];
        for(int i = 0; i < board.length; i++){
            for(int j = 0; j < board[0].length; j++){
                copyBoard[i][j] = board[i][j];
            }
        }
        for(int row = 0; row < board.length; row++){
            for(int col = 0; col < board[0].length; col++){
                int liveNeighbors = 0;
                for(int i = 0; i < 3; i++){
                    for(int j = 0; j < 3; j++){
                        if(neighbors[i] != 0 || neighbors[j] != 0){
                            int r = row + neighbors[i];
                            int c = col + neighbors[j];
                            if(r < board.length && r >= 0 && c < board[0].length && c >= 0 && copyBoard[r][c] == 1){
                                liveNeighbors++;
                            }
                        }
                    }
                }
                if(copyBoard[row][col] == 1 && (liveNeighbors < 2 || liveNeighbors > 3)) board[row][col] = 0;
                if(copyBoard[row][col] == 0 && liveNeighbors == 3) board[row][col] = 1;
            }
        } 
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.8 MB, 在所有 Java 提交中击败了53.60% 的用户

方法二

你不就想既可以保存原数组的状态，还可以更新新的状态吗？这些统统都可以在原有数组上搞。具体怎么搞呢？

  • 原来的 0 和 1 不就是代表死和生吗？但是你要更新新的状态，无非就是从生->死，从死->生。那我们加个状态 2，代表 生->死，加个状态 3 表示从 死>生。
  • 对于一个节点来说，如果它周边的点是 1 或者 2，就说明该点上一轮是活的。
  • 整体策略是完成 原始状态->过渡状态->真实状态 的过程。
  • 过渡状态 到 真实状态，代码就是把 0 和 2 变回 0，1 和 3 变回1的过程。用模只是代码技巧。
  • 策略实现的第一步是先找到当前节点周围的存活节点数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#Python
class Solution:
    def gameOfLife(self, board: List[List[int]]) -> None:
        #  原始状态 -> 过渡状态
        for i in range(len(board)):
            for j in range(len(board[0])):
                liveNeighbors = 0
                # 判断上边
                if i > 0:
                    if board[i - 1][j] == 1 or board[i - 1][j] == 2:
                        liveNeighbors += 1
                # 判断左边
                if j > 0:
                    if board[i][j - 1] == 1 or board[i][j - 1] == 2:
                        liveNeighbors += 1
                # 判断下边
                if i < len(board) - 1:
                    if board[i + 1][j] == 1 or board[i + 1][j] == 2:
                        liveNeighbors += 1
                # 判断右边
                if j < len(board[0]) - 1:
                    if board[i][j + 1] == 1 or board[i][j + 1] == 2:
                        liveNeighbors += 1
                # 判断左上角
                if i > 0 and j > 0:
                    if board[i - 1][j - 1] == 1 or board[i - 1][j - 1] == 2:
                        liveNeighbors += 1
                # 判断右下角
                if i < len(board) - 1 and j < len(board[0]) - 1:
                    if board[i + 1][j + 1] == 1 or board[i + 1][j + 1] == 2:
                        liveNeighbors += 1
                # 判断右上角
                if i > 0 and j < len(board[0]) - 1:
                    if board[i - 1][j + 1] == 1 or board[i - 1][j + 1] == 2:
                        liveNeighbors += 1
                # 判断左下角
                if i < len(board) - 1 and j > 0:
                    if board[i + 1][j - 1] == 1 or board[i + 1][j - 1] == 2:
                        liveNeighbors += 1
                # 根据周边存活数量更新当前点，结果是 0 和 1 的情况不用更新
                if board[i][j] == 0 and liveNeighbors == 3:
                    board[i][j] = 3
                elif board[i][j] == 1 and (liveNeighbors < 2 or liveNeighbors > 3):
                    board[i][j] = 2
        # 过渡状态 -> 真实状态
        for i in range(len(board)):
            for j in range(len(board[0])):
                board[i][j] = board[i][j] % 2

执行耗时:52 ms,击败了15.25% 的Python3用户
内存消耗:14.7 MB,击败了7.69% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Java
class Solution {
    public void gameOfLife(int[][] board) {
        for(int i = 0; i < board.length; i++){
            for(int j = 0; j < board[0].length; j++){
                int liveNeighbors = 0;
                if(i > 0 && (board[i-1][j] == 1 || board[i-1][j] == 2)) liveNeighbors++;
                if(j > 0 && (board[i][j-1] == 1 || board[i][j-1] == 2)) liveNeighbors++;
                if(i < board.length-1 && (board[i+1][j] == 1 || board[i+1][j] == 2)) liveNeighbors++;
                if(j < board[0].length-1 && (board[i][j+1] == 1 || board[i][j+1] == 2)) liveNeighbors++;
                if(i > 0 && j > 0 && (board[i-1][j-1] == 1 || board[i-1][j-1] == 2)) liveNeighbors++;
                if(i < board.length-1 && j < board[0].length-1 && (board[i+1][j+1] == 1 || board[i+1][j+1] == 2)) liveNeighbors++;
                if(i > 0 && j < board[0].length-1 && (board[i-1][j+1] == 1 || board[i-1][j+1] == 2)) liveNeighbors++;
                if(i < board.length-1 && j > 0 && (board[i+1][j-1] == 1 || board[i+1][j-1] == 2)) liveNeighbors++;
                if(board[i][j] == 0 && liveNeighbors == 3) board[i][j] = 3;
                else if(board[i][j] == 1 && (liveNeighbors < 2 || liveNeighbors > 3)) board[i][j] = 2;
            }
        }
        for(int i = 0; i < board.length; i++){
            for(int j = 0; j < board[0].length; j++) board[i][j] %= 2;
        }
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.5 MB, 在所有 Java 提交中击败了93.77% 的用户

30.搜索二维矩阵

第74题：搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。

该矩阵具有如下特性：

  • 每行中的整数从左到右按升序排列。
  • 每行的第一个整数大于前一行的最后一个整数。

示例 1:

1
2
3
4
5
6
7
8
9
输入:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3

输出: true

示例 2:

1
2
3
4
5
6
7
8
9
输入:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 13

输出: false

第一个条件意味着可以通过二分搜索确定哪行；

第二个条件意味着可以在行里进行二分搜索确定哪个元素；

方法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#Python
class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if len(matrix) == 0 or len(matrix[0]) == 0 or target < matrix[0][0] or target > matrix[-1][-1]:
            return False
        # 二分法找到target所在的行
        top, bottom = 0, len(matrix) - 1
        while top < bottom:
            mid = top + (bottom - top) // 2
            if matrix[mid][-1] < target:
                top = mid + 1
            else:
                bottom = mid
        # 在行里进行二分搜索确定哪个元素
        l, r = 0, len(matrix[top]) - 1
        while l <= r:
            mid = (l + r) // 2
            if matrix[top][mid] == target:
                return True
            elif matrix[top][mid] < target:
                l = mid + 1
            else:
                r = mid - 1
        return False

执行耗时:36 ms,击败了87.44% 的Python3用户
内存消耗:15 MB,击败了5.38% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//Java
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        int col = matrix[0].length;
        if(row == 0 || col == 0 || target < matrix[0][0] || target > matrix[row-1][col-1]) return false;
        int top = 0, bottom = row;
        while(top < bottom){
            int mid = (bottom + top) >> 1;
            if(matrix[mid][col-1] < target) top = mid + 1;
            else bottom = mid;
        }
        int left = 0, right = col;
        while(left < right){
            int mid = (right + left) >> 1;
            if(matrix[top][mid] < target) left = mid + 1;
            else right = mid;
        }
        return matrix[top][left] == target;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：37.6 MB, 在所有 Java 提交中击败了94.20% 的用户

方法二

根据题目特性直接将数组拉平，当作一个一维数组的二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#Python
class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if len(matrix) == 0 or len(matrix[0]) == 0 or target < matrix[0][0] or target > matrix[-1][-1]:
            return False
        m = len(matrix)
        n = len(matrix[0])
        # 根据题目特性直接将数组拉平，当作一个一维数组的二分查找
        l = 0
        r = m * n
        while l < r:
            mid = (l + r) // 2
            i = mid // n
            j = mid % n
            if target == matrix[i][j]:
                return True
            elif target > matrix[i][j]:
                l = mid + 1
            else:
                r = mid
        return False

执行耗时:32 ms,击败了96.26% 的Python3用户
内存消耗:15.1 MB,击败了5.38% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//Java
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length;
        int col = matrix[0].length;
        if(row == 0 || col == 0 || target < matrix[0][0] || target > matrix[row-1][col-1]) return false;
        int l = 0, r = row * col;
        while(l < r){
            int mid = (l + r) >> 1;
            if(matrix[mid / col][mid % col] < target) l = mid + 1;
            else r = mid;
        }
        return matrix[l / col][l % col] == target;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：37.5 MB, 在所有 Java 提交中击败了95.90% 的用户

31.子集

第78题：子集
给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明： 解集不能包含重复的子集

示例:

1
2
3
输入: nums = [1,2,3] 

输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

首先我们可以证明一下 N 个元素的子集个数有 2^N 个

可以类比为 N 个不同的小球，一次拿出若干个小球（可以不拿），对于每一个球都可以选择拿或者不拿，共有 N 个球，总共判断 N 次，产生了 2^N 个子集。

我们其实可以用二进制来模拟每个元素是否选中的状态。 又因为我们已知了对于 N 个元素共有 2^N 个子集，所以我们直接遍历 2^N 个元素。

但是我们并不知道具体的子集元素。那如何找到对应的子集元素呢？对于 2^N 个 N 位的二进制数，我们可以通过从后往前的第 j 个二进制位的 0 和 1 来表示是否放入子集集合。

方法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Python
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        k = len(nums)
        res = [[]]
        # 子集总数共有 2^N 个
        for i in range(1, 1 << k):
            # 找到对应的子集元素
            temp = []
            # 对于 2^N 个 N 位的二进制数，我们可以通过从后往前的第 j 个二进制位的 0 和 1 来表示是否放入子集集合。
            for j in range(k):
                if i >> j & 1:
                    temp.append(nums[j])
            res.append(temp)
        return res

执行耗时:40 ms,击败了66.14% 的Python3用户
内存消耗:14.9 MB,击败了5.37% 的Python3用户

为帮助大家理解，假设 nums 为 [1,2,3]，res 的存储过程为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//Java
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        int k = nums.length;
        List<List<Integer>> res = new ArrayList<>();
        for(int i = 0; i < (1 << k); i++){
            List<Integer> tmp = new ArrayList<>();
            for(int j = 0; j < k; j++){
                if(((i >> j) & 1) != 0) tmp.add(nums[j]);
            }
            res.add(tmp);
        }
        return res;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了87.14% 的用户
内存消耗：38.6 MB, 在所有 Java 提交中击败了75.78% 的用户

方法二：

直接遍历，遇到一个数就把所有子集加上该数组成新的子集

1
2
3
4
5
6
7
#Python
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = [[]]
        for i in range(len(nums) - 1, -1, -1):
            for subres in res[:]: res.append(subres + [nums[i]])
        return res

执行耗时:44 ms,击败了40.73% 的Python3用户
内存消耗:14.9 MB,击败了5.37% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//Java
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        res.add(new ArrayList<>());
        for(int i = 0; i < nums.length; i++){
            int all = res.size();
            for(int j = 0; j < all; j++){
                List<Integer> tmp = new ArrayList<>(res.get(j));
                tmp.add(nums[i]);
                res.add(tmp);
            }
        }
        return res;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了87.14% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了63.70% 的用户

方法三：

集合中所有元素的选/不选，其实构成了一个满二叉树。左子树选，右子树不选。自然，那从根节点到所有叶子节点的路径，就构成了所有的子集。

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        n = len(nums)
        def dfs(i, tmp):
            res.append(tmp)
            for j in range(i, n):
                dfs(j + 1, tmp + [nums[j]])
        dfs(0, [])
        return res

执行耗时:44 ms,击败了40.73% 的Python3用户
内存消耗:14.9 MB,击败了5.37% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Java
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums, new ArrayList<>());
        return res;
    }

    public void dfs(int index, int[] nums, List<Integer> tmp){
        res.add(tmp);
        for(int i = index; i < nums.length; i++){
            List<Integer> new_tmp = new ArrayList<>(tmp);
            new_tmp.add(nums[i]);
            dfs(i + 1, nums, new_tmp);
        }
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了87.14% 的用户
内存消耗：38.6 MB, 在所有 Java 提交中击败了73.80% 的用户

32.量出4升水

题目：量出4升水
怎么用3升和5升的桶量出4升的水？

题目没什么补充的，直接分析，一个3升和5升的水桶：

首先用三升水桶装满水，倒入五升水桶：

再次倒满三升水桶，填满后继续倒入五升水桶，直到五升水桶倒满。

清空五升水桶，将三升水桶的一升水倒入：

再次填满三升水桶，倒入五升水桶中：

33.最大的钻石

题目：最大的钻石
1 楼到 n 楼的每层电梯门口都放着一颗钻石，钻石大小不一。你乘坐电梯从 1 楼到 n 楼，每层楼电梯门都会打开一次，只能拿一次钻石，问怎样才能拿到「最大」的一颗？

面试时如果被问到这种题目，其实大多数面试官心中并没有一个标准答案。（不排除有面试官深究的）事实是作为面试者，我们只要流畅的给出答案，大概率都是可以顺利过关。

回到题目。其实题中包含一个隐藏条件：随机放置。所有的分析都是基于随机放置给出的。换句话说，如果放置钻石是人为干预大小，那么本题的所以分析则全部不成立。

其实这个问题的原型叫做秘书问题，该类问题全部属于最佳停止问题。

这类问题都有着统一的解法：

我们要选择先放弃前 37%（就是1/e）的钻石，此后选择比前 37% 都大的第一颗钻石。

其实该法则还有很多运用，比如一些常见的推文《谈恋爱拒绝掉前面37%的人》，其实就是一样的原因。

改题目还有一些变种，比如：

一个活动，n个女生手里拿着长短不一的玫瑰花，无序的排成一排，一个男生从头走到尾，试图拿更长的玫瑰花，一旦拿了一朵就不能再拿其他的，错过了就不能回头，问最好的策略?

现在要聘请 1 名秘书，共有 n 个应聘者，每面试 1 人后，就知道了应聘者的好坏程度，且必须立刻决定是否聘用，不可重复面试。策略是拒绝前 k 个应聘者，而从第 k+1 个应聘者开始，一旦有比前 k 个都好的，就立刻聘用。如何决定 k 的值，使得聘用到最佳应聘者的概率最大？等等。

这里再给出一个严谨的推导过程：

34.思维定势

下面这道题也是一道常见的智力题，但是这道题绝对不会出现在面试中了。拿出来分享给大家的原因，是期望不要被思维定势局限。

这道题中有六个停车位，每个车位上都有一个数字，然而有一个车位上的数字被汽车挡住了，要求学生们在20秒内答出这个被挡住的车位上的数字。这是中国香港小学一道给6岁儿童设计的“停车场智力题”。

答案：L8，即87

35.图的基础知识

图（Graph）是表示物件与物件之间的关系的数学对象，是图论的基本研究对象。

图是一个比树形关系复杂一点点，比线性关系复杂两点点的东东。

  • 线性关系是一对一：一个前驱一个后继。
  • 树形结构是一对多：一个父多个子
  • 图形结构是多对多：任意两个顶点（图中的节点叫做顶点）都有可能相关，是一种多对多的关系。

图我们一般表示为 G = (V，E)

  • V：代表点
  • E：代表边

啥意思嘞，比如就上面那个绿油油的图，就可以表示为:

  • V={1,2,3,4,5,6}
  • E={(1,2),(1,5),(2,3),(2,5),(3,4),(4,5),(4,6)}

图里最基本的单元是顶点（vertex），相当于树中的节点。顶点之间的关联关系，被称为边（edge）。而边可以分配一个数值（正负都ok），这个数值就叫做权重。

无向图和有向图

有方向的图就是有向图，无方向的图就是无向图。

完全图

所有的顶点互相连接在一起，那就是完全图。

在无向图中，若每对顶点之间都有一条边相连，则称该图为完全图。大概就是这样：

而在有向图中，若每对顶点之间都有二条有向边相互连接，也算是完全图。

循环图和DAG

循环图中的循环二字，指的是起点和终点是同一节点时产生的路径。所以，循环图和有向图或无向图并没有什么关系，因为都有可能产生循环。有向图，那就遵循边的方向。无向图，那只要成环就行。

这三个：

  • 第一个就是无向循环图
  • 第二个就是有向非循环图
  • 第三个就是有向循环图

第二个更多的是被称为有向无环图DAG（Directed Acyclic Graph）。下面这个也是 ：

那上面这个像不像一棵树。。。。。所以计算机结构中的树（大多都是有向的），其实就是一个DAG。

加权图

用数学语言讲，设G为图，对图的每一条边e来说，都对应于一个实数W(e)（可以通俗的理解为边的“长度”，只是在数学定义中图的权可以为负数），我们把W(e)称为e的“权”。把这样的图G称为“加权图”。

但是这里如果细分的话，又分为顶点加权图和边加权图。 说白了，就是有人发现如果只给边加上权值（就是长度）并不够用，有时候也需要给顶点加上权值。

连通图

在图论中，连通图基于连通的概念。在一个无向图 G 中，若从顶点i到顶点j有路径相连（当然从j到i也一定有路径），则称i和j是连通的。

连通的图，就是连通图：

如果不通了，就是非连通图：（这是一个图）

那没有连通在一起的这两坨（或者说移动的这两坨），我们叫作岛。

所以，如果我们的图里包含岛，那就是非连通图。

稠密图和稀疏图

如何定义稠密和稀疏？梵蒂冈也有人觉得他们的圣彼得大教堂拥挤，所以稠密稀疏本身就是一个主观定义。

我们可以简单的认为，稀疏图的边数远远少于完全图，反之，稠密图的边数接近于或等于完全图。

36.旋转图像

第48题：旋转图像
给定一个 n × n 的二维矩阵表示一个图像。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

方法一

一般容易想到的是，一层层的从外到内旋转每一圈（至于为什么不从内到外，如果你觉得方便，也ok），也就是俗称的找框框。

对每个框框，其实都有 4 个顶点：


交换完毕之后，再继续交换移动后的四个顶点：

那代码实现其实就很简单了：

  • 我们通过 x 和 y 就可以定义这个框框的边界
  • 找到框框后，我们再通过框框边界来定义出4个顶点
  • 然后完成交换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#Python
class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        x, y = 0, len(matrix[0]) - 1
        # 从最外圈开始到最内圈
        while x < y:
            s = x
            e = y
            # 每一圈每轮换4个顶点
            while s < y:
                matrix[x][s], matrix[e][x], matrix[y][e], matrix[s][y] \
                    = matrix[e][x], matrix[y][e], matrix[s][y], matrix[x][s]
                s += 1
                e -= 1
            x += 1
            y -= 1
        return matrix

执行耗时:36 ms,击败了81.13% 的Python3用户
内存消耗:14.8 MB,击败了38.77% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//Java
class Solution {
    public void rotate(int[][] matrix) {
        int x = 0, y = matrix[0].length - 1;
        while(x < y){
            int s = x, e = y;
            while(s < y){
                swap(matrix, x, s, e, x);
                swap(matrix, e, x, y, e);
                swap(matrix, y, e, s, y);
                s++;
                e--;
            }
            x++;
            y--;
        }
    }

    public void swap(int[][] matrix, int x1, int y1, int x2, int y2){
        int tmp = matrix[x1][y1];
        matrix[x1][y1] = matrix[x2][y2];
        matrix[x2][y2] = tmp;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了26.87% 的用户

方法二

我们观察这个矩阵，向右旋转90°，是不是可以理解为先上下翻转，再沿对角线翻转：

1
2
3
4
5
6
7
8
9
10
11
#Python
class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        # 上下翻转
        for i in range(len(matrix)//2):
            matrix[i], matrix[len(matrix)-i-1] = matrix[len(matrix)-i-1], matrix[i]
        # 对角线翻转
        for i in range(len(matrix)):
            for j in range(i+1, len(matrix)):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        return matrix

执行耗时:32 ms,击败了93.70% 的Python3用户
内存消耗:14.8 MB,击败了34.93% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//Java
class Solution {
    public void rotate(int[][] matrix) {
        for(int i = 0; i < matrix.length / 2; i++){
            int[] tmp = matrix[i];
            matrix[i] = matrix[matrix.length - i - 1];
            matrix[matrix.length - i - 1] = tmp;
        }

        for(int i = 0; i < matrix.length; i++){
            for(int j = i + 1; j < matrix.length; j++){
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = tmp;
            }
        }
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：38.7 MB, 在所有 Java 提交中击败了22.51% 的用户

37.螺旋矩阵II

第59题：螺旋矩阵Ⅱ
给定一个正整数 n，生成一个包含 1 到 $n^2$ 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例：

1
2
输入: 3
输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]

题目理解较为容易，给定 n = 3，那就生成一个 3^2 = 9 的矩阵。大家看下面的图可能更加直观一些：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#Python
class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        res = [[0 for _ in range(n)] for _ in range(n)]
        x, y = 0, n - 1
        count = 1
        # 从外圈到里圈
        while x <= y:
            # 向右取
            for j in range(x, y + 1):
                res[x][j] = count
                count += 1
            # 向下取
            for i in range(x + 1, y + 1):
                res[i][y] = count
                count += 1
            # 向左取
            for j in range(y - 1, x - 1, -1):
                res[y][j] = count
                count += 1
            # 向上取
            for i in range(y - 1, x, -1):
                res[i][x] = count
                count += 1
            x += 1
            y -= 1
        return res

执行耗时:44 ms,击败了33.33% 的Python3用户
内存消耗:14.7 MB,击败了22.80% 的Python3用户

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//Java
class Solution {
    public int[][] generateMatrix(int n) {
        int[][] res = new int[n][n];
        int count = 1, x = 0, y = n - 1;
        while(x <= y){
            for(int j = x; j <= y; j++) res[x][j] = count++;
            for(int i = x + 1; i <= y; i++) res[i][y] = count++;
            for(int j = y - 1; j >= x; j--) res[y][j] = count++;
            for(int i = y - 1; i > x; i--) res[i][x] = count++;
            x++;
            y--;
        }
        return res;
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00% 的用户
内存消耗：36.6 MB, 在所有 Java 提交中击败了32.38% 的用户

排序系列

1.排序专栏

所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。是《数据结构与算法》中最基本的算法之一。

我们常说的十大排序算法为：冒泡、选择、插入、希尔、归并、快速、堆、计数、桶、基数

基本分类
我们常根据是否可以在线性时间内比较对其分类：

时间复杂度

如何记忆时间复杂度呢？

  1. 平方阶 (O(n2)) 插入、选择、冒泡
  2. 线性对数阶 (O(nlog2n)) 快速、归并、堆
  3. 特殊的希尔 O(n^(1.3—2))
  4. 牛皮的线性 基数、桶、箱、计数

啥是稳定：

稳定：如果 a 原本在 b 前面，而 a=b，排序之后 a 仍然在 b 的前面。
不稳定：如果 a 原本在 b 的前面，而 a=b，排序之后 a 可能会出现在 b 的后面。

哪些稳定：

稳定：冒泡、插入、归并和基数。 不稳定：选择、快速、希尔、堆。

2.冒泡排序

冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

作为最简单的排序算法之一，冒泡排序给我的感觉就像 Abandon 在单词书里出现的感觉一样，每次都在第一页第一位，所以最熟悉。冒泡排序还有一种优化算法，就是立一个 flag，当在一趟序列遍历中元素没有发生交换，则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用。

算法步骤

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
    最慢和最快

正序时最快，反序时最慢

1
2
3
4
5
6
7
8
9
10
#Python
def bubbleSort(arr):
    for i in range(len(arr) - 1):
    	flag = True
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
                flag = False
        if flag: break 
    return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//Java
import java.util.Arrays;

public class BubbleSort {
    public static void bubbleSort(int[] arr){
        for(int i=0; i<arr.length-1; i++){
            boolean flag = true;
            for(int j=0; j< arr.length-i-1; j++){
                if(arr[j] > arr[j+1]){
                    int tmp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = tmp;
                    flag = false;
                }
            }
            if (flag) break;
        }
    }

    public static void main(String[] args) {
        int[] arr = {9,3,1,4,6,8,7,5,2};
        bubbleSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

3.基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

基数排序 vs 计数排序 vs 桶排序

基数排序有两种方法：

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异案例看大家发的：

  • 基数排序：根据键值的每位数字来分配桶；
  • 计数排序：每个桶只存储单一键值；
  • 桶排序：每个桶存储一定范围的数值；

LSD 基数排序动图演示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#Python
def radix(arr):
    digit = 0
    max_digit = 1
    max_value = max(arr)
    # 找出列表中最大的位数
    while 10**max_digit < max_value:
        max_digit = max_digit + 1 
    while digit < max_digit:
        # 创建桶
        temp = [[] for i in range(10)]
        for i in arr:
            # 求出每一个元素的个、十、百位直到最高位的值
            t = int((i/10**digit)%10)
            # 添加进相应的桶中
            temp[t].append(i)
        # 将桶中的数据依次取出
        coll = []
        for bucket in temp:
            for i in bucket:
                coll.append(i)
        # 作为下次装桶的数据        
        arr = coll
        # 直到遍历完所有位
        digit = digit + 1
    return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
//java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class RadixSort {
    /**
     * 获取最高位数
     */
    private static int getMaxDigit(int[] arr) {
        int maxValue = getMaxValue(arr);
        return getNumLenght(maxValue);
    }

    private static int getMaxValue(int[] arr) {
        int maxValue = arr[0];
        for (int value : arr) {
            if (maxValue < value) {
                maxValue = value;
            }
        }
        return maxValue;
    }

    private static int getNumLenght(long num) {
        if (num == 0) {
            return 1;
        }
        int lenght = 0;
        for (long temp = num; temp != 0; temp /= 10) {
            lenght++;
        }
        return lenght;
    }

    private static int[] radixSort(int[] arr) {
        int mod = 10;
        int dev = 1;
        int maxDigit = getMaxDigit(arr);

        for (int i = 0; i < maxDigit; i++, dev *= 10) {
            // 考虑负数的情况，这里扩展一倍队列数，其中 [0-9]对应负数，[10-19]对应正数 (bucket + 10)
            List<Integer>[] counter = new List[mod * 2];
            for (int j = 0; j < arr.length; j++) {
                // 求每位的余数，并加10，使得负数映射到0-9，正数映射到10-19
                int bucket = (arr[j] / dev % mod) + mod;
                if(counter[bucket] == null) counter[bucket] = new ArrayList<>();
                counter[bucket].add(arr[j]);
            }
            //将桶中的数按顺序取出，进行下一位的排序
            int pos = 0;
            for (List<Integer> bucket : counter) {
                if(bucket != null) {
                    for (int value : bucket) {
                        arr[pos++] = value;
                    }
                }
            }
        }
        return arr;
    }

    public static void main(String[] args) {
        int[] arr = {-5, -3, 6, 8, 1, 7, 9, 4, 2, -9};
        System.out.println(Arrays.toString(radixSort(arr)));
    }
}

4.选择排序

选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。

算法步骤

  1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  3. 重复第二步，直到所有元素均排序完毕。
1
2
3
4
5
6
7
8
9
10
11
12
#Python
def selectionSort(arr):
    for i in range(len(arr) - 1):
        # 记录最小数的索引
        minIndex = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[minIndex]:
                minIndex = j
        # i 不是最小数时，将 i 和最小数进行交换
        if i != minIndex:
            arr[i], arr[minIndex] = arr[minIndex], arr[i]
    return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//Java
import java.util.Arrays;

public class SelectionSort {
    public static void selectSort(int[] arr){
        for(int i=0; i<arr.length-1; i++){
            int minPos = i;
            for(int j=i+1; j<arr.length; j++){
                minPos = arr[j] < arr[minPos]? j: minPos;
            }
            int tmp = arr[i];
            arr[i] = arr[minPos];
            arr[minPos] = tmp;
        }
    }

    public static void main(String[] args) {
        int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
        selectSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

5.插入排序

插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了，因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

插入排序和冒泡排序一样，也有一种优化算法，叫做拆半插入。

算法步骤

  1. 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
  2. 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
1
2
3
4
5
6
7
8
9
10
#Python
def insertionSort(arr):
    for i in range(len(arr)):
        preIndex = i-1
        current = arr[i]
        while preIndex >= 0 and arr[preIndex] > current:
            arr[preIndex+1] = arr[preIndex]
            preIndex-=1
        arr[preIndex+1] = current
    return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//Java
import java.util.Arrays;

public class InsertionSort {
    public static void insertionSort(int[] arr){
        for(int i=1; i< arr.length; i++){
            int tmp =  arr[i];
            int j = i;
            while(j > 0 && tmp < arr[j-1]){
                arr[j] = arr[j-1];
                j--;
            }
            if(j != i) arr[j] = tmp;
        }
    }
    public static void main(String[] args) {
        int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
        insertionSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

6.希尔排序

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

希尔排序过程
希尔排序的基本思想是：将数组列在一个表中并对列分别进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身还是使用数组进行排序。
例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样(竖着的元素是步长组成)：

1
2
3
4
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

1
2
3
4
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]。这时10已经移至正确位置了，然后再以3为步长进行排序：

1
2
3
4
5
6
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之后变为：

1
2
3
4
5
6
10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最后以1步长进行排序（此时就是简单的插入排序了）

希尔排序的分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#Python
def shellSort(arr):
    n = len(arr)
    # 初始步长
    gap=1
    while(gap < len(arr)/3):
        gap = gap*3+1
    while gap > 0:
        # 按步长进行划分
        for i in range(gap, n):
            j = i
            # 对每列进行插入排序
            while j >= gap and arr[j - gap] > arr[j]:
                arr[j - gap], arr[j] = arr[j], arr[j - gap]
                j -= gap
        # 得到新的步长
        gap = gap // 3
    return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//Java
import java.util.Arrays;

public class ShellSort {
    public static void shellSort(int[] arr){
        int gap = 1;
        while (gap < arr.length/3) {
            gap = gap * 3 + 1;
        }
        while(gap > 0) {
            for(int i=gap; i < arr.length; i++){
                int tmp = arr[i];
                int j = i - gap;
                while(j >= 0 && arr[j] > tmp){
                    arr[j+gap] = arr[j];
                    j -= gap;
                }
                arr[j+gap] = tmp;
            }
            gap /= 3;
        }
    }

    public static void main(String[] args) {
        int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
        shellSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

7.归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：

  • 自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）；
  • 自下而上的迭代；

在《数据结构与算法 JavaScript 描述》中，作者给出了自下而上的迭代方法。但是对于递归法，作者却认为：

However, it is not possible to do so in JavaScript, as the recursion goes too deep for the language to handle.

然而，在 JavaScript 中这种方式不太可行，因为这个算法的递归深度对它来讲太深了。

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。

算法步骤

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  4. 重复步骤 3 直到某一指针达到序列尾；
  5. 将另一序列剩下的所有元素直接复制到合并序列尾。

动图演示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#Python
def mergeSort(alist):
    if len(alist) <= 1:
        return alist
    # 二分分解
    num = len(alist)//2
    left = mergeSort(alist[:num])
    right = mergeSort(alist[num:])
    # 合并
    return merge(left,right)

def merge(left, right):
    '''合并操作，将两个有序数组left[]和right[]合并成一个大的有序数组'''
    #left与right的下标指针
    l, r = 0, 0
    result = []
    while l<len(left) and r<len(right):
        if left[l] <= right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]
    result += right[r:]
    return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//Java
import java.util.Arrays;

public class MergeSort {
    public static int[] mergeSort(int[] arr){
        if (arr.length < 2) {
            return arr;
        }
        int middle = arr.length / 2;

        int[] left = mergeSort(Arrays.copyOfRange(arr, 0, middle));
        int[] right = mergeSort(Arrays.copyOfRange(arr, middle, arr.length));

        return merge(left, right);
    }

    public static int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        int i = 0, l = 0, r = 0;
        while (l < left.length && r < right.length) {
            if (left[l] <= right[r]) result[i++] = left[l++];
            else result[i++] = right[r++];
        }
        while (l < left.length) result[i++] = left[l++];
        while (r < right.length) result[i++] = right[r++];

        return result;
    }

    public static void main(String[] args) {
        int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
        System.out.println(Arrays.toString(mergeSort(arr)));
    }
}

8.快速排序

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较，但这种状况并不常见。事实上，快速排序通常明显比其他 Ο(nlogn) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

快速排序的名字起的是简单粗暴，因为一听到这个名字你就知道它存在的意义，就是快，而且效率高！它是处理大数据最快的排序算法之一了。虽然 Worst Case 的时间复杂度达到了 O(n²)，但是人家就是优秀，在大多数情况下都比平均时间复杂度为 O(nlogn) 的排序算法表现要更好：

快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

算法步骤

  1. 从数列中挑出一个元素，称为 “基准”（pivot）;
  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

动图演示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#Python
def quick_sort(alist, start, end):
    """快速排序"""
    # 递归的退出条件
    if start >= end:
        return
    # 设定起始元素为要寻找位置的基准元素
    mid = alist[start]
    # low为序列左边的由左向右移动的游标
    low = start
    # high为序列右边的由右向左移动的游标
    high = end
    while low < high:
        # 如果low与high未重合，high指向的元素不比基准元素小，则high向左移动
        while low < high and alist[high] >= mid:
            high -= 1
        # 将high指向的元素放到low的位置上
        alist[low] = alist[high]
        # 如果low与high未重合，low指向的元素比基准元素小，则low向右移动
        while low < high and alist[low] < mid:
            low += 1
        # 将low指向的元素放到high的位置上
        alist[high] = alist[low]
    # 退出循环后，low与high重合，此时所指位置为基准元素的正确位置
    # 将基准元素放到该位置
    alist[low] = mid
    # 对基准元素左边的子序列进行快速排序
    quick_sort(alist, start, low-1)
    # 对基准元素右边的子序列进行快速排序
    quick_sort(alist, low+1, end)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//Java
import java.util.Arrays;

public class QuickSort {

    public void quickSort(int[] arr, int start, int end) {
        if(start >= end) return;
        //设定基准
        int pivot = arr[start];
        int low = start;
        int high = end;
        while(low < high){
            while(low < high && arr[high] >= pivot) high--;
            arr[low] = arr[high];
            while(low < high && arr[low] <= pivot) low++;
            arr[high] = arr[low];
        }
        arr[low] = pivot;
        quickSort(arr, start, low - 1);
        quickSort(arr, low + 1, end);
    }

    public static void main(String[] args) {
        int[] arr = {8, 7, 2 ,1, 9};
        new QuickSort().quickSort(arr, 0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
}
//sout: [1, 2, 7, 8, 9]

9.堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

  1. 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
  2. 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

算法步骤

  1. 将待排序序列构建成一个堆 H[0……n-1]，根据（升序降序需求）选择大顶堆或小顶堆；
  2. 把堆首（最大值）和堆尾互换；
  3. 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
  4. 重复步骤 2，直到堆的尺寸为 1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#Python
#大顶堆
def heapify(arr, i, length):
    left = 2 * i + 1
    right = 2 * i + 2
    maxIndex = i
    if left < length and arr[left] > arr[maxIndex]:
        maxIndex = left
    if right < length and arr[right] > arr[maxIndex]:
        maxIndex = right
    if maxIndex != i:
        arr[i], arr[maxIndex] = arr[maxIndex], arr[i]
        heapify(arr, maxIndex, length)

def heapSort(arr):
    n = len(arr)
    # 初始化大顶堆
    for i in range(len(arr) // 2 - 1 , -1, -1):
        heapify(arr, i, n)
    for i in range(len(arr) - 1, 0, -1):
        # 根节点为最大
        arr[0], arr[i] =  arr[i], arr[0]
        # 换出根节点后 再对剩下的排序 最后形成升序
        n -= 1
        heapify(arr, 0, n)
    return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Java
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Queue;

public class HeapSort {

    public static int[] heapSort(int[] arr){
        Queue<Integer> heap = new PriorityQueue<>();
        for(int num: arr) heap.offer(num);
        for(int i = 0; i < arr.length; i++) arr[i] = heap.poll();
        return arr;
    }

    public static void main(String[] args) {
        int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
        System.out.println(Arrays.toString(heapSort(arr)));
    }
}

10.计数排序

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

算法步骤

  1. 找出原数组中元素值最大的，记为max。
  2. 创建一个新数组count，其长度是max加1，其元素默认值都为0。
  3. 遍历原数组中的元素，以原数组中的元素作为count数组的索引，以原数组中的元素出现次数作为count数组的元素值。
  4. 创建结果数组result，起始索引index。
  5. 遍历count数组，找出其中元素值大于0的元素，将其对应的索引作为元素值填充到result数组中去，每处理一次，count中的该元素值减1，直到该元素值不大于0，依次处理count中剩下的元素。
  6. 返回结果数组result。

1
2
3
4
5
6
7
8
9
10
11
12
#Python
def countingSort(arr):
    maxLen = max(arr) + 1
    count = [0 for i in range(maxLen)]
    result = []
    for i in arr:
        count[i] += 1
    for i in range(maxLen):
        while count[i] > 0:
            result.append(i)
            count[i] -= 1
    return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//Java
import java.util.Arrays;

public class CountSort {
    public static int[] countSort(int[] arr){
        if(arr.length < 2) return arr;
        int maxValue = arr[0];
        for (int i : arr) maxValue=i > maxValue?i: maxValue;
        int[] count = new int[maxValue+1];
        int[] res = new int[arr.length];
        for (int i : arr) count[i]++;
        for(int i=0, j=0; i<=maxValue; i++){
            while(count[i]-- > 0) res[j++]=i;
        }
        return res;
    }

    public static void main(String[] args) {
        int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
        System.out.println(Arrays.toString(countSort(arr)));
    }
}

这里有个问题：上述写法并不是稳定排序，因此这里做改进，稳定的计数排序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//Java
import java.util.Arrays;

public class CountSort {
    public static int[] countSort(int[] arr){
        if(arr.length < 2) return arr;
        int maxValue = arr[0];
        for (int i : arr) maxValue = i > maxValue?i: maxValue;
        int[] count = new int[maxValue+1];
        int[] res = new int[arr.length];
        for (int i : arr) count[i]++;
        //做累加，使桶中记录的为每个数的最后一个索引
        for (int i=1; i<=maxValue; i++) count[i] = count[i] + count[i-1];
        //逆序遍历，直接往相应索引填数，使得算法稳定
        for (int i=arr.length-1; i>=0; i--){
            res[--count[arr[i]]] = arr[i];
        }
        return res;
    }

    public static void main(String[] args) {
        int[] arr = {5, 3, 6, 8, 1, 7, 9, 4, 2};
        System.out.println(Arrays.toString(countSort(arr)));
    }
}

11.桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

  1. 在额外空间充足的情况下，尽量增大桶的数量
  2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

什么时候最快

当输入的数据可以均匀的分配到每一个桶中。

什么时候最慢

当输入的数据被分配到了同一个桶中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#Python
def bucket_sort(array, bucketSize=5):
    # bucketSize设置每个桶的容量
    maxValue = max(array)
    minValue = min(array)
    # 1.创建空桶
    bucketCount = (maxValue - minValue) // bucketSize + 1
    buckets = [[] for _ in range(bucketCount)]
    # 2.利用映射函数将数据分配到各个桶中
    for data in array:
        index = (int)(data - minValue) // bucketSize
        buckets[index].append(data)

    # 3.桶内排序
    for i in range(bucketCount):
        buckets[i].sort()

    # 4.产生新的排序后的列表
    index = 0
    for i in range(bucketCount):
        for j in range(len(buckets[i])):
            array[index] = buckets[i][j]
            index += 1
    return array
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
//Java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;

public class BucketSort {
    //bucketSize用于设置每个桶的容量
    public int[] bucketSort(int[] arr, int bucketSize){
        if (arr.length == 0) return arr;
        //得到数组中的最大，最小值
        int minValue = arr[0];
        int maxValue = arr[0];
        for (int value : arr) {
            if (value < minValue) {
                minValue = value;
            } else if (value > maxValue) {
                maxValue = value;
            }
        }
        //多少个桶
        int bucketCount = (maxValue - minValue) / bucketSize + 1;
        //创建空桶
        List<Integer>[] buckets = new List[bucketCount];
        for (int value : arr) {
            //映射函数，存放到相应桶中
            int index = (value - minValue) / bucketSize;
            if(buckets[index] == null) buckets[index] = new ArrayList<Integer>();
            buckets[index].add(value);
        }
        //对每个桶排序
        for (List<Integer> bucket : buckets) {
            //桶不为空
            if(bucket != null) Collections.sort(bucket);
        }
        //产生排序后的新列表
        int[] res = new int[arr.length];
        int index = 0;
        for (List<Integer> bucket : buckets){
            //桶不为空
            if(bucket != null) {
                for (Integer integer : bucket) {
                    res[index] = integer;
                    index++;
                }
            }
        }
        return res;
    }

    public static void main(String[] args) {
        int[] arr = {8, 7, 2 ,1, 9};
        int[] res = new BucketSort().bucketSort(arr, 3);
        System.out.println(Arrays.toString(res));
    }

}