前言

本次解析src/dropout.h和src/dropout.c两个文件，也即是Dropout层。

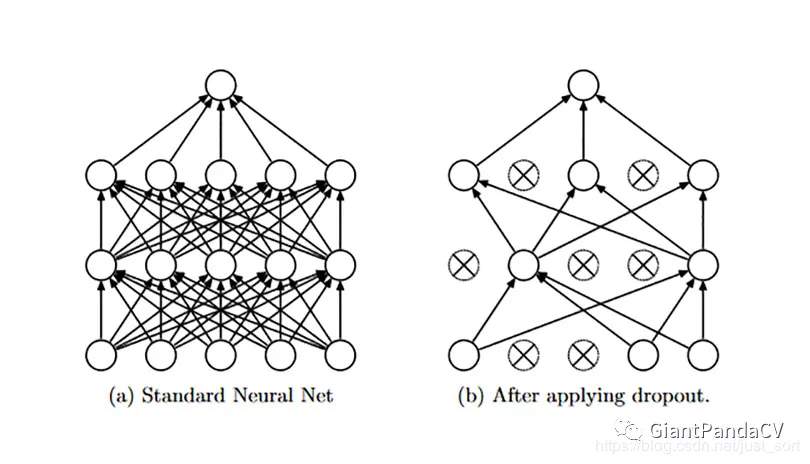
Dropout

在CNN中使用Dropout分成训练和测试两个阶段，在训练阶段，Dropout以一定的概率$p$随机丢弃一部分神经元节点，即这部分神经元节点不参与计算，如下图所示。

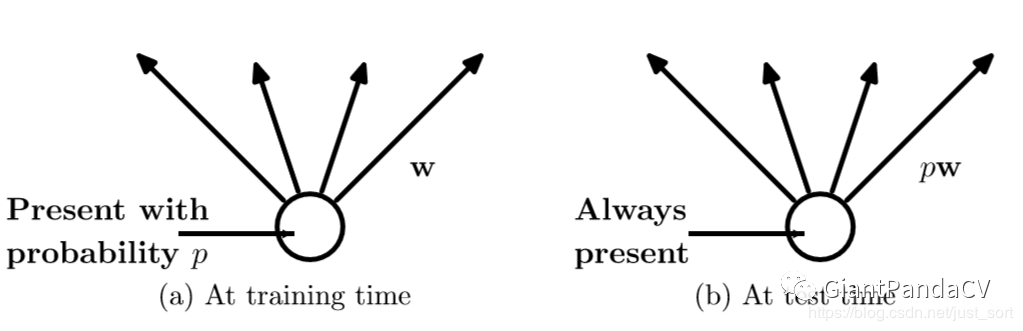
在训练时，每个神经元有概率$p$的可能性被保留下来，即Dropout的丢弃概率为$1-p$。在测试阶段，每个神经元都是存在的，权重参数$w$要乘以$p$成为$pw$。为什么测试阶段要乘以$p$呢？

考虑第一个隐藏层的一个神经元在Dropout之前的输出是$x$，那么Dropout之后的期望值为$E=px+(1-p)0$，在测试时该神经元总是激活的，为了保持同样的输出期望值并使得下一层也得到同样的结果，需要调整$x->px$。其中$p$是Bernoulli分布（0-1分布）中值为1的概率。示意图如下：

Inverted Dropout

在训练的时候由于舍弃一些神经元，因此在测试的时候需要在激活的结果中乘上因子$p$进行缩放，但是这样需要对测试的代码进行修改并增加了测试时的运算量，十分影响测试时的性能。通常为了提高测试的性能，可以将缩放的工作转移到训练阶段，而测试阶段和不使用Dropout一致，这一操作就被叫作Inverted Dropout。具体实现的时候只需要将前向传播Dropout时保留下来的神经元的权重乘上$\frac{1}{p}$即可。

代码解析

dropout_layer.h代码解析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include "layer.h"
#include "network.h"

typedef layer dropout_layer;

#ifdef __cplusplus
extern "C" {
#endif
// 构建一个dropout层
dropout_layer make_dropout_layer(int batch, int inputs, float probability, int dropblock, float dropblock_size_rel, int dropblock_size_abs, int w, int h, int c);

// dropout前向传播
void forward_dropout_layer(dropout_layer l, network_state state);
// dropout反向传播
void backward_dropout_layer(dropout_layer l, network_state state);
void resize_dropout_layer(dropout_layer *l, int inputs);

#ifdef GPU
void forward_dropout_layer_gpu(dropout_layer l, network_state state);
void backward_dropout_layer_gpu(dropout_layer l, network_state state);

#endif
#ifdef __cplusplus
}
#endif
#endif

dropout_layer.cpp代码解析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
/*
 * 构建dropout层
 * batch 一个batch中图片张数
 * inputs  dropout层每张输入图片的元素个数
 * probability dropout概率,即某个输入神经元被丢弃的概率,由配置文件指定;如果配置文件中未指定,则默认值为0.5(参见parse_dropout_layer()函数)
 * 返回dropout_layer
 *
 * 说明: dropout层的构建函数需要的输入参数比较少,网络输入数据尺寸h,w,c也不需要;
 * 注意: dropout层有l.inputs = l.outputs; 另外此处实现使用了inverted dropout, 不是标准的dropout
 */
dropout_layer make_dropout_layer(int batch, int inputs, float probability, int dropblock, float dropblock_size_rel, int dropblock_size_abs, int w, int h, int c)
{
    dropout_layer l = { (LAYER_TYPE)0 };
    l.type = DROPOUT;
    l.probability = probability; //丢弃概率 (1-probability 为保留概率)
    l.dropblock = dropblock; 
    l.dropblock_size_rel = dropblock_size_rel;
    l.dropblock_size_abs = dropblock_size_abs;
    if (l.dropblock) {
        l.out_w = l.w = w;
        l.out_h = l.h = h;
        l.out_c = l.c = c;

        if (l.w <= 0 || l.h <= 0 || l.c <= 0) {
            printf(" Error: DropBlock - there must be positive values for: l.w=%d, l.h=%d, l.c=%d \n", l.w, l.h, l.c);
            exit(0);
        }
    }
    l.inputs = inputs; // dropout层不会改变输入输出的个数,因此有 l.inputs == l.outputs
    l.outputs = inputs; // 虽然dropout会丢弃一些输入神经元, 但这丢弃只是置该输入元素值为0, 并没有删除
    l.batch = batch; // 一个batch中图片数量
    l.rand = (float*)xcalloc(inputs * batch, sizeof(float)); //动态分配内存,
    l.scale = 1./(1.0 - probability); //使用inverted dropout, scale取保留概率的倒数
    l.forward = forward_dropout_layer; //前向传播
    l.backward = backward_dropout_layer; // 反向传播
    #ifdef GPU
    l.forward_gpu = forward_dropout_layer_gpu;
    l.backward_gpu = backward_dropout_layer_gpu;
    l.rand_gpu = cuda_make_array(l.rand, inputs*batch);
    #endif
    if (l.dropblock) {
        if(l.dropblock_size_abs) fprintf(stderr, "dropblock       p = %.2f   l.dropblock_size_abs = %d         %4d  ->   %4d\n", probability, l.dropblock_size_abs, inputs, inputs);
        else fprintf(stderr, "dropblock       p = %.2f   l.dropblock_size_rel = %.2f         %4d  ->   %4d\n", probability, l.dropblock_size_rel, inputs, inputs);
    }
    else fprintf(stderr, "dropout       p = %.2f                  %4d  ->   %4d\n", probability, inputs, inputs);
    return l;
}

void resize_dropout_layer(dropout_layer *l, int inputs)
{
    l->inputs = l->outputs = inputs;
    l->rand = (float*)xrealloc(l->rand, l->inputs * l->batch * sizeof(float));
    #ifdef GPU
    cuda_free(l->rand_gpu);

    l->rand_gpu = cuda_make_array(l->rand, l->inputs*l->batch);
    #endif
}

/*
 * dropout层前向传播函数
 * @l 当前dropout层函数
 * @state 整个网络
 *
 * 说明:dropout层没有训练参数,因此前向传播函数比较简单,只需要完成一件事: 按指定概率 l.probability
 * 丢弃输入元素,并将保留下来的输入元素乘以比例因子scale(采用inverted dropout, 这种凡是实现更为方便,
 * 且代码接口比较统一;如果采用标准的dropout, 则测试阶段需要进入 forward_dropout_layer(),
 * 使每个输入乘以保留概率,而使用inverted dropout, 测试阶段就不需要进入到forward_dropout_layer())
 *
 * 说明: dropout层有l.inputs = l.outputs;
 */

void forward_dropout_layer(dropout_layer l, network_state state)
{
    int i;
	// 因为使用inverted dropout,所以测试阶段不需要进入forward_dropout_layer()
    if (!state.train) return;
    for(i = 0; i < l.batch * l.inputs; ++i){
		// 采样一个0-1之间均匀分布的随机数
        float r = rand_uniform(0, 1);
        l.rand[i] = r; // 每一个随机数都要保存到l.rand,之后反向传播时候会用到
        if(r < l.probability) state.input[i] = 0; // 舍弃该元素,将其值置为0, 所以这里元素的总个数并没有发生变化;
        else state.input[i] *= l.scale; //保留该输入元素,并乘以比例因子scale
    }
}

/*
 * dropout层反向传播函数
 * l 当前dropout层网络
 * state 整个网络
 *
 * 说明: dropout层的反向传播相对简单,因为其本身没有训练参数,也没有激活函数,或者说激活函数为f(x) =x,
 * 也就是激活函数关于加权输入的导数值为1, 因此其自身的误差项值以后由下一层网络反向传播时计算完了,
 * 没有必要再曾以激活函数关于加权输入的导数了.剩下要做的就是计算上一层的误差项net.delta, 这个计算也很简单;
 */
void backward_dropout_layer(dropout_layer l, network_state state)
{
    int i;
	// 如果state.delta为空,则返回(state.delta为空则说明已经反向传播到第一层了,此处所指定的第一层,是state.layers[0]
    // 也就是与输入层直接相连的第一层隐含层, 详细见 network.c 中的 forward_network()函数)
    if(!state.delta) return;
    for(i = 0; i < l.batch * l.inputs; ++i){
		// 与前向过程 forward_dropout_layer 照应,根据l.rand指示,
        float r = l.rand[i];
		// 如果r <　probability,说明舍丢弃的输入，其误差项值为0
        if(r < l.probability) state.delta[i] = 0;
		// 保留下的输入元素,其误差项值为当前层对应输出的误差项值乘以l.scale
        else state.delta[i] *= l.scale;
    }
}