如何减少卷积层计算量,使用宽卷积的好处及转置卷积中的棋盘效应
如何减少卷积层计算量?
减少卷积层的计算量主要有以下几种方法:
- 使用池化操作。在卷积层前使用池化操作降低特征图分辨率。
使用堆叠的小卷积核代替大卷积核。VGG16中使用2个3 x 3卷积代替一个5 x 5卷积。
使用深度可分离卷积。将原始的$K \times K \times C$的卷积核分成$K \times K \times 1$和$1 \times 1 \times C$两部分操作。
应用1 x 1卷积。将1 x 1卷积(假设通道数为$C_2$)直接应用在某个卷积层(假设维度为$K \times K \times C_{1}$)之前
使用宽卷积的好处?
所谓宽卷积就是指在卷积操作时填充方式为same方式。而与之对应的窄卷积就是指在卷积操作时填充方式为valid方式。same方式的填充通常使用0填充的方式对卷积核不满足整除条件的输入特征图进行补全,使得卷积层的输出维度和输入维度一致。valid方式的填充就是不进行任何填充,在输入特征边缘位置若不足以进行卷积操作,则对边缘信息进行舍弃,因此在步长为1的情况下该填充方式的卷积层输出特征维度可能会略小于输入特征的维度。我们可以发现宽卷积(same填充方式卷积)的好处就是通过补0操作可以有效的保留原始输入特征图的边界特征信息。
转置卷积和棋盘效应?
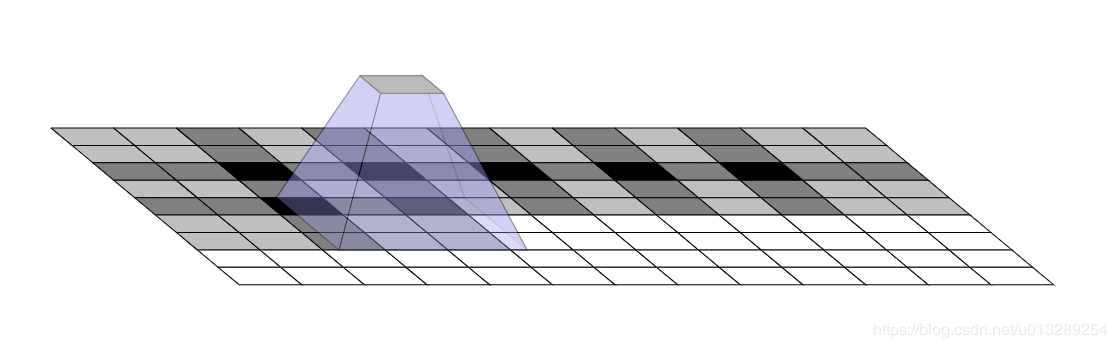
当我们在用反卷积(转置卷积)做图像生成或者上采样的时候或许我们会观察到我们生成的图片会出现一些奇怪的棋盘图案或者说你感觉到你生成的图片有颗粒感。棋盘格效应趋向于出现在图像中最显著的地方 (颜色最强烈),如下图所示:

这种现象之所以会发生是因为在上采样使用反卷积的时候,卷积核的大小不能被步长整除导致的。先看一下没有棋盘效应的情况:

再看一下出现棋盘效应的情况:

即它很容易遇到一种叫做 “uneven overlap”(不均匀重叠) 的现象。具体来说, 当kernel_size 无法被 stride整除时, 反卷积就会出现这种不均匀重叠的现象。原则上,神经网络可以通过仔细学习权值来避免这种情况,但在实践中,神经网络很难完全避免这种情况.
并且在二维图片上棋盘效应会更加严重。
因此为了避免棋盘效应的发生,一般有一下几种解决方案:
方法1:现在,神经网络在创建图像时通常使用多层反卷积,从一系列较低分辨率的描述中迭代地构建较大的图像。虽然这些堆叠的反卷积可能会消除棋盘效应,但它们通常会复合,从而在各种尺度上产生棋盘效应。
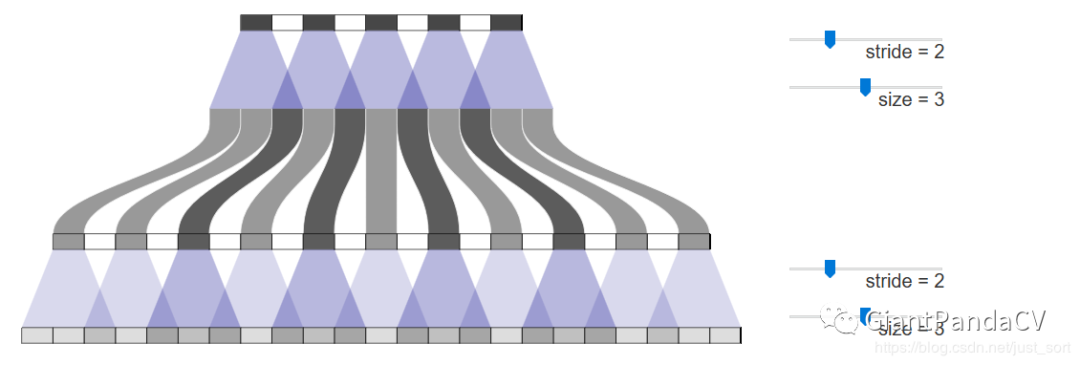
方法2:在反卷积后面,再接一个步长为1的卷积,效果有限。
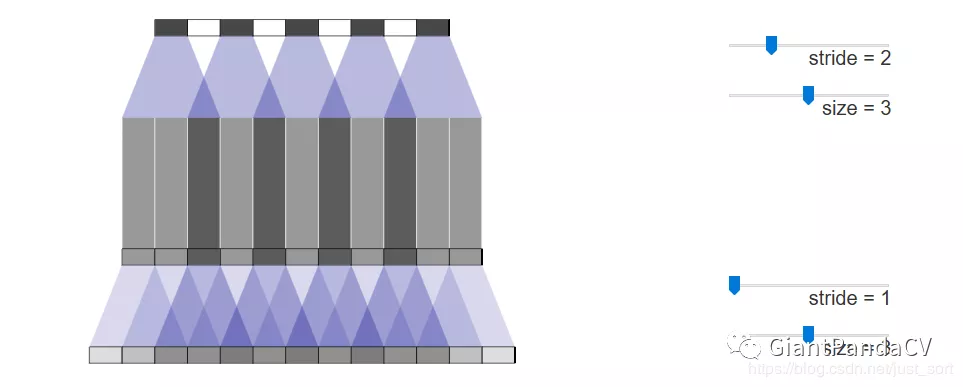
方法3:调整卷积核的权重,适当加大重叠部分少的权重,虽然理论有效,但在实际操作中,不仅有困难也会减弱模型的表达力。
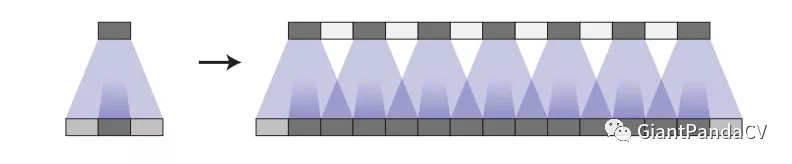
方法4:使得卷积核大小能被步长整除,但卷积核权重的学习不均匀也会导致棋盘效应现象(下图为步长为2,核大小为4所产生的棋盘效应现象)
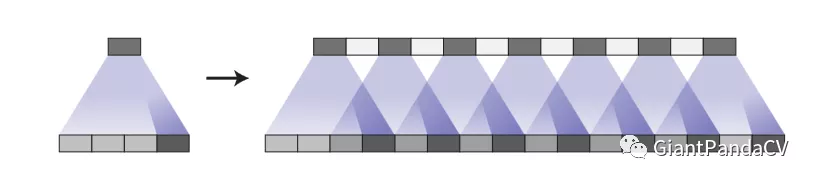
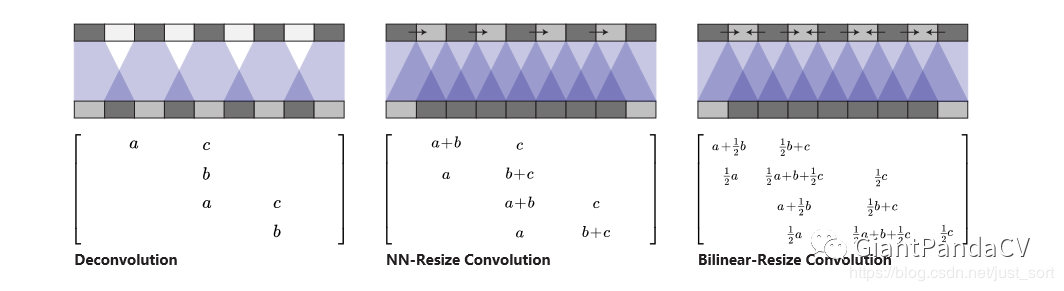
方法5:调整图像大小(使用最近邻插值或双线性插值),然后执行卷积操作。这似乎是一种自然的方法,大致相似的方法在图像超分辨率方面表现良好。
总结
假设反卷积生成的图像中,包含1只黑猫,黑猫身体部分的像素颜色应该是平滑过渡的。或者极端的说,身体部分应该全部都是黑色的。而在实际生成的图像中,该部分却是由深深浅浅的近黑方块组成的,很像棋盘的网络。这就是所谓的棋盘效应。之所以会出现棋盘效应是因为插入的值为0,使得卷积的input feature map本身就是棋盘状,所以得到的大分辨率feature map也会产生棋盘格。反卷积产生的棋盘格,在stride和卷积核size是整数倍的时候能够有所缓解,因为二者整除关系使得卷积核每次滑动能用到的非零像素的个数是一样的或者中间区域向两边逐渐减少(而不是随着滑动反复变化产生棋盘格形状),但是依然不能完全消除。
从原始英文博客上的实验结论来看,使用上采样+卷积层的图像放大方法有效的改善了棋盘效应,即不是将小分辨率的feature map的像素之间插0,而是采用插值的方法,所以要是图像生成的时候遇到了棋盘效应你知道怎么做了吗?Upsamping+Convolution来帮你。

